题目内容
某种商品,现在定价p元,每月卖出n件,设定价上涨x成,每月卖出数量减少y成,每月售货总金额变成现在的z倍.
(1)用x和y表示z;
(2)设x与y满足y=kx(0<k<1),利用k表示当每月售货总金额最大时x的值;
(3)若y= x,求使每月售货总金额有所增加的x值的范围.
x,求使每月售货总金额有所增加的x值的范围.
(1)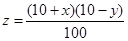 ;(2)
;(2)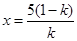 ;(3)(0,5)。
;(3)(0,5)。
解析试题分析:(1)利用等量关系建立解析式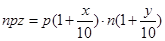 ,化简得
,化简得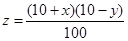 ;(2)由y=kx(0<k<1)代入解析式
;(2)由y=kx(0<k<1)代入解析式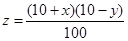 转化为二次函数
转化为二次函数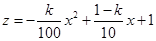 的最值问题,在对称轴
的最值问题,在对称轴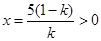 处取得最大值;(3)使每月售货总金额有所增加即
处取得最大值;(3)使每月售货总金额有所增加即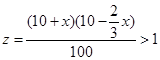 ,转化为不等式的问题来求解,解得0<x<5。
,转化为不等式的问题来求解,解得0<x<5。
试题解析:(1)按现在的定价上涨x成时,上涨后的定价为p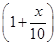 元,每月卖出数量为n
元,每月卖出数量为n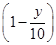 件,每月售货总金额是npz元,
件,每月售货总金额是npz元,
因而npz=p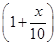 ·n
·n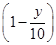 ,所以
,所以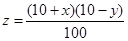 。
。
(2)在y=kx的条件下,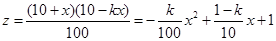 ,
,
对称轴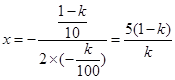 ,
,
∵0<k<1,∴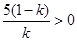 . ∴当
. ∴当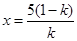 时,z有最大值。
时,z有最大值。
(3)当y= x时,
x时,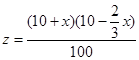 ,
,
要使每月售货总金额有所增加,即z>1,
应有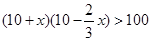 ,即x(x-5)<0.所以0<x<5.
,即x(x-5)<0.所以0<x<5.
所以所求x的范围是(0,5).
考点:二次函数的最值问题与不等式的求解问题以及转化与化归的思想。

练习册系列答案
相关题目
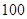
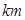 ,按交通法规定:这段公路车速限制在
,按交通法规定:这段公路车速限制在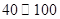 (单位:
(单位: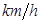 )之间.假设目前油价为
)之间.假设目前油价为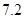 (单位:元
(单位:元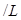 ),汽车的耗油率为
),汽车的耗油率为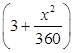 (单位:
(单位: ), 其中
), 其中 (单位:
(单位: 元,不考虑其它费用,这次租车的总费用最少是多少?此时的车速
元,不考虑其它费用,这次租车的总费用最少是多少?此时的车速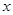 元,则本年度新增用电量
元,则本年度新增用电量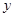 (亿千瓦时)与
(亿千瓦时)与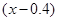 元成反比例.又当
元成反比例.又当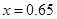 时,
时,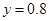 .
.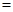 用电量
用电量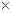 (实际电价-成本价)]
(实际电价-成本价)]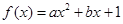 (
( 为实数,
为实数,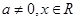 ),
),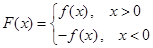 ,⑴若
,⑴若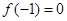 ,且函数
,且函数 的值域为
的值域为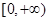 ,求
,求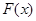 的表达式;
的表达式; ,且函数
,且函数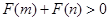 .
.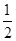 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用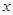 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数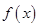 .
.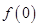 的值,并解释其实际意义;
的值,并解释其实际意义;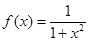 ,现有
,现有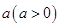 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.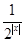 +2.
+2.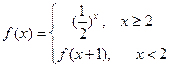 ,则函数
,则函数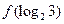 的值为
的值为
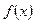 的图象经过点(9,
的图象经过点(9,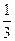 ), 则f(25)的值是_________.
), 则f(25)的值是_________.