题目内容
【题目】某班抽取20名学生周测物理考试成绩(单位:分)的频率分布直方图如下:
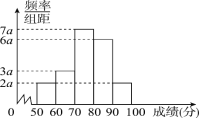
(1)求频率分布直方图中a的值,并写出众数;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中任选2人,求这2人的成绩都在[60,70)中的概率.
【答案】(1)a=0.005.众数:75(2)2,3 (3)![]() .
.
【解析】
(1)由频率分布直方图中小矩形面积和为1,求出a,再根据众数的定义计算即可得到答案.(2)利用频率分布直方图能求出成绩落在[50,60)与[60,70)中的学生人数.
(3)利用列举法得到成绩在[50,70)的学生中任选2人的基本事件总数以及此2人成绩都在[60,70)中包含的基本事件数,由概率公式计算即得到答案.
(1)据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,
解得a=0.005,众数:75
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3
(3)记成绩落在[50,60)中的2人为A1,A2,成绩落在[60,70)中的3人为B1,B2,B3,
则从成绩在[50,70)的学生中任选2人的基本事件共有10个:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(B1,B2),(B1,B3),(B2,B3),
记“两人成绩都落在[60,70)”为事件C,
则事件C包含的基本事件有3个:(B1,B2),(B1,B3),(B2,B3),
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表: 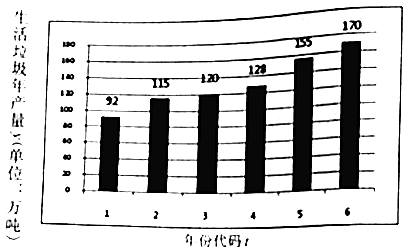
2016年初 | 2016年末 | |
社区A | 539 | 568 |
社区B | 543 | 585 |
社区C | 568 | 600 |
社区D | 496 | 513 |
注1:年份代码1~6分别对应年份2011~2016
注2:参与度= ![]() ×100%
×100%
参与度的年增加值=年末参与度﹣年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为 ![]() =14.8t+
=14.8t+ ![]() ,预测2020年该年生活垃圾的产生量;
,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题: ①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?