题目内容
15.设对一切实数x有f(x+$\frac{1}{2}$)=$\frac{1}{2}$+$\sqrt{f(x+\frac{1}{2})-{f}^{2}(x+\frac{1}{2})}$,证明f(x)是周期函数.分析 根据已知,利用平方法去除根号化简得:函数为常数函数,进而得到结论.
解答 证明:∵对一切实数x有f(x+$\frac{1}{2}$)=$\frac{1}{2}$+$\sqrt{f(x+\frac{1}{2})-{f}^{2}(x+\frac{1}{2})}$,
∴f(x+$\frac{1}{2}$)-$\frac{1}{2}$=$\sqrt{f(x+\frac{1}{2})-{f}^{2}(x+\frac{1}{2})}$,
则f(x+$\frac{1}{2}$)≥$\frac{1}{2}$,且f2(x+$\frac{1}{2}$)-f(x+$\frac{1}{2}$)+$\frac{1}{4}$=f(x+$\frac{1}{2}$)-f2(x+$\frac{1}{2}$),
即2f2(x+$\frac{1}{2}$)-2f(x+$\frac{1}{2}$)+$\frac{1}{4}$=0
解得:f(x+$\frac{1}{2}$)=$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$,
即f(x)是常数函数,任意正实数均为函数的周期;
点评 本题考查的知识点是函数的周期性,其中得到函数是常数函数是解答的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
5.将甲、乙、丙三位新同学分到2个不同的班级,每班至少1人,则甲、乙被分到同一个班的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
6.已知F1,F2分别是中心在坐标原点,对称轴为做标轴的双曲线C的左、右焦点,过F2的直线l与双曲线的右支交于A,B两点,I1,I2分别为△AF1F2,△BF1F2的内心,若双曲线C的离心率为2,|I1I2|=$\frac{9}{2}$,直线l的倾斜角的正弦值为$\frac{8}{9}$,则双曲线C的方程为( )
| A. | x${\;}^{2}+\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{48}$=1 | C. | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
10.已知函数f(x)=sin(ωx+$\frac{π}{6}$),其中ω>0,若f($\frac{π}{6}$)=f($\frac{π}{3}$),且f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)上有最小值、无最大值,则ω等于( )
| A. | $\frac{40}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{4}{3}$ |
5.已知复数z=x+2i(x∈R,i为虚数单位),z2=-3+4i,则x=( )
| A. | ±1 | B. | -1 | C. | 0 | D. | 1 |
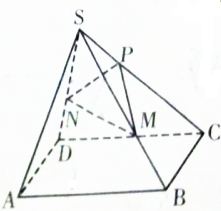 如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.