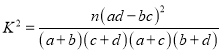题目内容
【题目】一片成熟森林的总面积为![]() (近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
(近期内不再种植),计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的![]() ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
【答案】(1)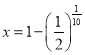 ;(2)砍伐了 5年;(3)今后最多还能砍伐15年.
;(2)砍伐了 5年;(3)今后最多还能砍伐15年.
【解析】试题分析:
(1)设每年砍伐面积的百分比为![]() ,由题意及指数函数的知识得
,由题意及指数函数的知识得![]()
![]() ,解得
,解得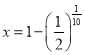 ,即为所求。(2)设经过
,即为所求。(2)设经过![]() 年剩余面积为原来的
年剩余面积为原来的![]() ,可得方程
,可得方程![]() ,解得
,解得![]() 。(3)设从今年开始,以后砍了
。(3)设从今年开始,以后砍了![]() 年,则
年,则![]() 年后剩余面积为
年后剩余面积为![]() .由
.由![]() ,化简得
,化简得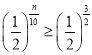 ,解得
,解得![]() ,即今后最多还能砍伐15年,由此可得结论。
,即今后最多还能砍伐15年,由此可得结论。
试题解析:
(1)设每年砍伐面积的百分比为![]() ,
,
则![]() ,即
,即![]() ,
,
解得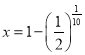 .
.
(2)设经过![]() 年剩余面积为原来的
年剩余面积为原来的![]() ,
,
由题意可得![]() ,
,
由(1)得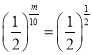 ,即
,即![]() ,
,
解得![]() ,
,
故到今年为止,已砍伐了 5年.
(3)设从今年开始,以后砍了![]() 年,则
年,则![]() 年后剩余面积为
年后剩余面积为![]() .
.
令![]() ,
,
即![]() ,
,
化简得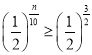 ,可得
,可得![]() ,
,
解得![]() .
.
故今后最多还能砍伐15年.

【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系.某重点高中数学教师对高三年级的50名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有22人,余下的人中,在高三年级模拟考试中数学平均成绩不足120分钟的占![]() ,统计成绩后,得到如下
,统计成绩后,得到如下![]() 的列联表:
的列联表:
分数大于等于120分钟 | 分数不足120分 | 合计 | |
周做题时间不少于15小时 | 4 | 22 | |
周做题时间不足15小时 | |||
合计 | 50 |
(Ⅰ)请完成上面的![]() 列联表,并判断能否有99%以上的把握认为“高中生的数学成绩与学生自主学习时间有关”;
列联表,并判断能否有99%以上的把握认为“高中生的数学成绩与学生自主学习时间有关”;
(Ⅱ)(ⅰ)按照分层抽样,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
(ii) 若将频率视为概率,从全校大于等于120分的学生中随机抽取人,求这些人中周做题时间不少于15小时的人数的期望和方差.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |