题目内容
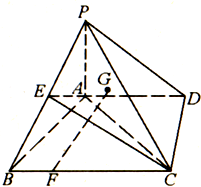 如图所示,PA⊥平面ABCD,∠ADC=90°,AD∥BC,AB⊥AC,且AB=AC=2,G为△PAC的重心,E为PB的中点,F在线段BC上,且CF=2FB.
如图所示,PA⊥平面ABCD,∠ADC=90°,AD∥BC,AB⊥AC,且AB=AC=2,G为△PAC的重心,E为PB的中点,F在线段BC上,且CF=2FB.(1)求证:FG∥平面PAB;
(2)求证:FG⊥AC;
(3)当PA长度为多少时,FG⊥平面ACE?
分析:(1)利用线面平行的判定定理或面面平行的性质证明.
(2)利用线面垂直的性质证明.(3)利用线面垂直的判定定理求值.
(2)利用线面垂直的性质证明.(3)利用线面垂直的判定定理求值.
解答: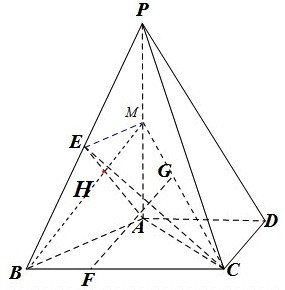 解:(1)连接CG交AP于M点,连接BM.
解:(1)连接CG交AP于M点,连接BM.
∵
=
=
,
∴FG∥BM,
又BM?平面PAB,FG?平面PAB
∴FG∥平面PAB.
(2)∵PA⊥平面ABCD,
∴PA⊥AC,
又∵AC⊥AB,PA∩AB=A.
∴AC⊥平面PAB,∴AC⊥BM,
∵FG∥BM,∴FG⊥AC.
(3)连结EM,由(2)知FG⊥AC,若FG⊥平面ACE,
则FG⊥AE,即BM⊥AE,又EM=
AB=1,
设EA∩BM=H,则EH=
HA,
设PA=a,则EA=
PB=
,EH=
EA=
.
因为Rt△AME~Rt△MHE,
所以EM2=EH•EA,
即1=
?
,解得a=
=2
.
即PA=2
时,FG⊥平面ACE.
 解:(1)连接CG交AP于M点,连接BM.
解:(1)连接CG交AP于M点,连接BM.∵
| CG |
| GM |
| CF |
| BF |
| 2 |
| 1 |
∴FG∥BM,
又BM?平面PAB,FG?平面PAB
∴FG∥平面PAB.
(2)∵PA⊥平面ABCD,
∴PA⊥AC,
又∵AC⊥AB,PA∩AB=A.
∴AC⊥平面PAB,∴AC⊥BM,
∵FG∥BM,∴FG⊥AC.
(3)连结EM,由(2)知FG⊥AC,若FG⊥平面ACE,
则FG⊥AE,即BM⊥AE,又EM=
| 1 |
| 2 |
设EA∩BM=H,则EH=
| 1 |
| 2 |
设PA=a,则EA=
| 1 |
| 2 |
| 1 |
| 2 |
| 4+a2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 4+a2 |
因为Rt△AME~Rt△MHE,
所以EM2=EH•EA,
即1=
| 1 |
| 2 |
| 4+a2 |
| 1 |
| 6 |
| 4+a2 |
| 8 |
| 2 |
即PA=2
| 2 |
点评:本题主要考查线面平行和线面垂直的判定,熟练掌握重心定理及线面平行、垂直的判定定理及性质定理是解决问题的关键.

练习册系列答案
相关题目
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.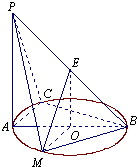 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC. 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形, 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.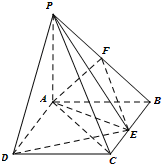 如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.