题目内容
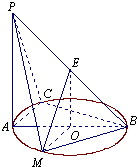 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.(1)求证:平面MOE∥平面PAC;
(2)求证:BC⊥平面PAC;
(3)求直线PB与平面PAC所成的角的正弦值.
分析:(1)先证明OE∥平面PAC、OM∥平面PAC,再利用面面平行的判定,可得平面MOE∥平面PAC;
(2)利用线线垂直证明线面垂直;
(3)由(2)知BC⊥面PAC,可得∠BPC为直线PB与平面PAC所成的角,求出BC、PB的值可得结论.
(2)利用线线垂直证明线面垂直;
(3)由(2)知BC⊥面PAC,可得∠BPC为直线PB与平面PAC所成的角,求出BC、PB的值可得结论.
解答:(1)证明:因为点E为线段PB的中点,点O为线段AB的中点,所以OE∥PA …(1分)
因为PA?平面PAC,OE?平面PAC,所以OE∥平面PAC.…(2分)
因为OM∥AC,因为AC?平面PAC,OM?平面PAC,所以OM∥平面PAC.…(3分)
因为OE∩OM=O,所以平面MOE∥平面PAC …(5分)
(2)证明:因为点C在以AB为直径的⊙O上,所以∠ACB=90°,即BC⊥AC,
因为PA⊥平面ABC,BC?平面ABC,所以PA⊥BC.…(7分)
因为PA∩AC=A,所以BC⊥平面PAC;…(9分)
(3)解:由(2)知BC⊥面PAC,∴∠BPC为直线PB与平面PAC所成的角.…(10分)
在Rt△PAC中,PC=
=
,
在Rt△ABC中,BC=
=
,
在Rt△PBC中,P=
=2
…(12分)
∴sin∠BPC=
=
=
.
∴直线PB与平面PAC所成的角的正弦值为
…(14分)
因为PA?平面PAC,OE?平面PAC,所以OE∥平面PAC.…(2分)
因为OM∥AC,因为AC?平面PAC,OM?平面PAC,所以OM∥平面PAC.…(3分)
因为OE∩OM=O,所以平面MOE∥平面PAC …(5分)
(2)证明:因为点C在以AB为直径的⊙O上,所以∠ACB=90°,即BC⊥AC,
因为PA⊥平面ABC,BC?平面ABC,所以PA⊥BC.…(7分)
因为PA∩AC=A,所以BC⊥平面PAC;…(9分)
(3)解:由(2)知BC⊥面PAC,∴∠BPC为直线PB与平面PAC所成的角.…(10分)
在Rt△PAC中,PC=
| PA2+AC2 |
| 5 |
在Rt△ABC中,BC=
| AB2-AC2 |
| 3 |
在Rt△PBC中,P=
| PC2+BC2 |
| 2 |
∴sin∠BPC=
| BC |
| PB |
| ||
2
|
| ||
| 4 |
∴直线PB与平面PAC所成的角的正弦值为
| ||
| 4 |
点评:本题考查面面平行,考查线面垂直,考查线面角,解题的关键是掌握面面平行、线面垂直的判定方法,属于中档题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.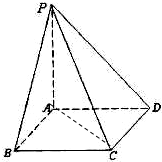 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,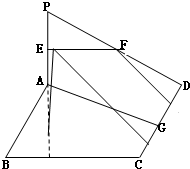 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.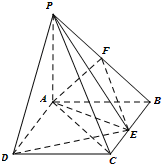 如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.