题目内容
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.(1)求证:BD⊥平面PAC.
(2)求二面角B-AN-C的正切值.
分析:(1)由已知中PA⊥平面ABCD,底面ABCD为菱形,结合菱形的性质及线面垂直的性质,我们可得BD⊥AC且BD⊥PA,再由线面垂直的判定定理可得BD⊥平面PAC;
(2)由(1)的结论,作OM⊥NA,连接BM,可得∠BMO为二面角B-AN-C的平面角,解RT△BMO,即可得到二面角B-AN-C的平面角的大小.
(2)由(1)的结论,作OM⊥NA,连接BM,可得∠BMO为二面角B-AN-C的平面角,解RT△BMO,即可得到二面角B-AN-C的平面角的大小.
解答: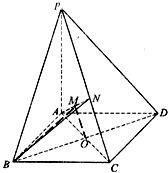 证明:(1)∵ABCD为菱形,
证明:(1)∵ABCD为菱形,
∴BD⊥AC
又∵PA⊥平面ABCD,BD?平面ABCD,
∴BD⊥PA
∵PA∩AC=A
∴BD⊥平面PAC;
解:(2)由(l)可知,BO⊥平面PAC,
故在平面PAC内,作OM⊥NA,
连接BM(如图),则∠BMO为二面角B-AN-C的平面角.
在RT△BMO中,易知AO=
,OM=
∴tan∠BMO=
,
即二面角B-AN-C的正切值为
 证明:(1)∵ABCD为菱形,
证明:(1)∵ABCD为菱形,∴BD⊥AC
又∵PA⊥平面ABCD,BD?平面ABCD,
∴BD⊥PA
∵PA∩AC=A
∴BD⊥平面PAC;
解:(2)由(l)可知,BO⊥平面PAC,
故在平面PAC内,作OM⊥NA,
连接BM(如图),则∠BMO为二面角B-AN-C的平面角.
在RT△BMO中,易知AO=
| 3 |
| ||
| 2 |
∴tan∠BMO=
| 6 |
即二面角B-AN-C的正切值为
| 6 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定,其中(1)的关键是证得BD⊥AC且BD⊥PA,(2)的关键是找到二面角B-AN-C的平面角∠BMO.

练习册系列答案
相关题目
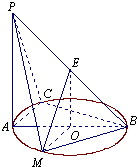 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.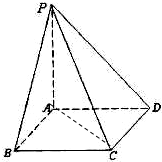 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,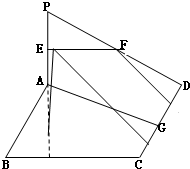 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.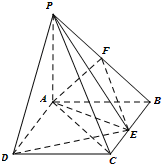 如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.