题目内容
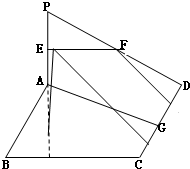 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(Ⅰ)求异面直线EF与AG所成角的余弦值;
(Ⅱ)求证:BC∥面EFG;
(Ⅲ)求三棱锥E-AFG的体积.
分析:(Ⅰ)判断∠DAG是EF与AG所成的角,然后直接求异面直线EF与AG所成角的余弦值;
(Ⅱ)首先证明BC∥EF,然后证明BC∥面EFG;
(Ⅲ)通过VE-AFG=VG-AEF,即可求三棱锥E-AFG的体积.
(Ⅱ)首先证明BC∥EF,然后证明BC∥面EFG;
(Ⅲ)通过VE-AFG=VG-AEF,即可求三棱锥E-AFG的体积.
解答:解:(Ⅰ)解:因为E,F分别是PA,PD的中点,所以EF∥AD,
于是,∠DAG是EF与AG所成的角…(2分)
∵AD=2,DG=1,AG=
,
∴cos∠DAG=
,
∴EF与AG所成角的余弦值是
…(4分)
(Ⅱ)证明:因为BC∥AD,AD∥EF,所以BC∥EF…(6分)
∵BC?平面EFG,EF?平面EFG,
∴BC∥平面EFG…(8分)
(Ⅲ)解:VE-AFG=VG-AEF=
S△AEF•DG=
…(12分)
于是,∠DAG是EF与AG所成的角…(2分)
∵AD=2,DG=1,AG=
| 5 |
∴cos∠DAG=
2
| ||
| 5 |
∴EF与AG所成角的余弦值是
2
| ||
| 5 |
(Ⅱ)证明:因为BC∥AD,AD∥EF,所以BC∥EF…(6分)
∵BC?平面EFG,EF?平面EFG,
∴BC∥平面EFG…(8分)
(Ⅲ)解:VE-AFG=VG-AEF=
| 1 |
| 3 |
| 1 |
| 12 |
点评:本题考查直线与平面平行的判定,几何体的体积的求法,两条直线的夹角的求法,考查空间想象能力,计算能力.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.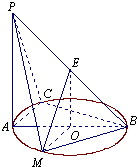 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.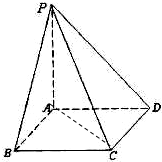 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,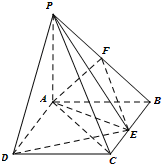 如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.