题目内容
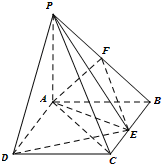 如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是边长为1的正方形.点F是PB的中点,点E在边BC上移动.(1)当点E为BC的中点时,试在AB上找一点G,使得平面PAC∥平面EFG.求此时AG的长度;
(2)证明:无论点E在边BC的何处,都有PE⊥AF.
分析:(1)当G为AB中点时,平面PAC∥平面EFG,连接GF,GE,证明GE∥平面PAC,EF∥平面PAC即可;
(2)无论点E在边BC的何处,证明AF⊥平面PBC,从而都有PE⊥AF.
(2)无论点E在边BC的何处,证明AF⊥平面PBC,从而都有PE⊥AF.
解答: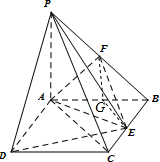 (1)解:当G为AB中点时,平面PAC∥平面EFG,连接GF,GE,
(1)解:当G为AB中点时,平面PAC∥平面EFG,连接GF,GE,
∵G为AB中点,E为BC的中点,
∴GE∥AC,
∵GE?平面PAC,AC?平面PAC,
∴GE∥平面PAC,
同理EF∥平面PAC,
∵GE∩EF=E,
∴平面PAC∥平面EFG,此时,AG=
;
(2)证明:∵PA⊥平面ABCD,
∴PA⊥AB,PA⊥BC,
∵PA=AB=1,F为PB的中点,
∴AF⊥PB,
∵BC⊥AB,AB∩PA=A,
∴BC⊥平面PAB,
∵AF?平面PAB,
∴BC⊥AF,
∵BC∩PB=B,AF⊥PB,BC⊥AF,
∴AF⊥平面PBC,
∵PE?平面PBC,
∴AF⊥PE.
 (1)解:当G为AB中点时,平面PAC∥平面EFG,连接GF,GE,
(1)解:当G为AB中点时,平面PAC∥平面EFG,连接GF,GE,∵G为AB中点,E为BC的中点,
∴GE∥AC,
∵GE?平面PAC,AC?平面PAC,
∴GE∥平面PAC,
同理EF∥平面PAC,
∵GE∩EF=E,
∴平面PAC∥平面EFG,此时,AG=
| 1 |
| 2 |
(2)证明:∵PA⊥平面ABCD,
∴PA⊥AB,PA⊥BC,
∵PA=AB=1,F为PB的中点,
∴AF⊥PB,
∵BC⊥AB,AB∩PA=A,
∴BC⊥平面PAB,
∵AF?平面PAB,
∴BC⊥AF,
∵BC∩PB=B,AF⊥PB,BC⊥AF,
∴AF⊥平面PBC,
∵PE?平面PBC,
∴AF⊥PE.
点评:本题考查线面平行,面面平行的判定,考查线面垂直,线线垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,PA=AB=2,N为PC的中点.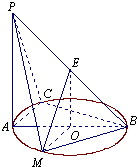 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,,点E为线段PB的中点,点M在AB弧上,且OM∥AC.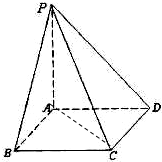 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形, 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.