题目内容
已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2-2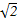
ρcos(θ-
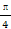)=2.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程.
(2)求经过两圆交点的直线的极坐标方程.
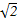ρcos(θ-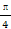)=2.(1)把圆O1和圆O2的极坐标方程化为直角坐标方程.
(2)求经过两圆交点的直线的极坐标方程.
(1) x2+y2-2x-2y-2=0 (2) ρsin(θ+
)=
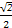
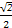
)=(1)∵ρ=2,∴ρ2=4,即x2+y2=4.
∵ρ2-2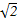ρcos(θ-)=2,
∴ρ2-2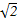ρ (cosθcos+sinθsin)=2.
∴x2+y2-2x-2y-2=0.
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x+y=1.化为极坐标方程为ρcosθ+ρsinθ=1,即ρsin(θ+)=.
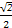∵ρ2-2
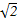ρcos(θ-)=2,∴ρ2-2
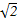ρ (cosθcos+sinθsin)=2.∴x2+y2-2x-2y-2=0.
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x+y=1.化为极坐标方程为ρcosθ+ρsinθ=1,即ρsin(θ+
)=.
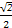练习册系列答案
相关题目
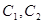的极坐标方程分别为
，
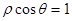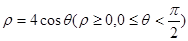则曲线
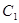与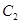
交点的极坐标为 ．
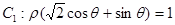与曲线
的一个交点在极轴上，则
的值为__________．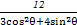
,点F1,F2为其左、右焦点,直线l的参数方程为
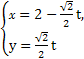(t为参数,t∈R).
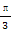(ρ∈R). (2)ρcos2
=1.
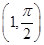
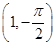
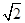sin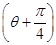 
，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
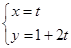(t为参数)，判断直线l和圆C的位置关系．
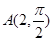，点
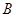在直线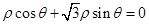
上运动，则线段
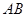的最短长度为 .
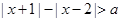有实数解，则实数
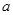的取值范围是 .
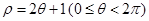与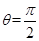
的交点的极坐标为 ．