题目内容
将下列各极坐标方程化为直角坐标方程.
(1)θ=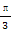 (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1.
(1)θ=
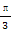 (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1.(1) y=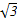 x (2) y2=-4(x-1)
x (2) y2=-4(x-1)
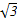 x (2) y2=-4(x-1)
x (2) y2=-4(x-1)(1)∵tanθ= ,∴tan
,∴tan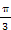 =
= =
=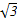 ,
,
化简得:y=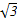 x.
x.
(2)∵ρcos2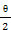 =1,∴ρ
=1,∴ρ =1.
=1.
即ρ+ρcosθ=2,所以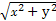 +x=2.
+x=2.
化简得y2=-4(x-1).
 ,∴tan
,∴tan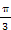 =
= =
=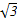 ,
,化简得:y=
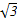 x.
x.(2)∵ρcos2
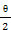 =1,∴ρ
=1,∴ρ =1.
=1.即ρ+ρcosθ=2,所以
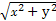 +x=2.
+x=2.化简得y2=-4(x-1).

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
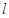 :
: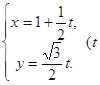 为参数), 曲线
为参数), 曲线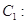
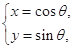 (
(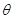 为参数).
为参数).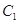 相交于
相交于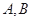 两点,求
两点,求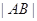 ;
;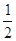 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的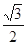 倍,得到曲线
倍,得到曲线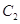 ,设点
,设点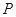 是曲线
是曲线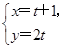 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为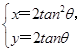 (θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.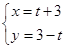 (参数t
(参数t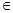 R).圆的参数方程为
R).圆的参数方程为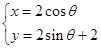 (参数
(参数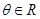 ),则圆C的圆心到直线l的距离为______.
),则圆C的圆心到直线l的距离为______.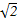 ρcos(θ-
ρcos(θ-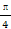 )=2.
)=2.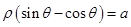 与曲线
与曲线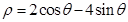 相交于
相交于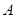 、
、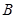 两点,若
两点,若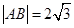 ,则实数
,则实数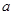 的值为 .
的值为 .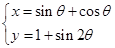 (θ为参数)有两个不同的交点,则实数a的取值范围为 .
(θ为参数)有两个不同的交点,则实数a的取值范围为 .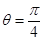 (
(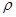 ∈R),它与曲线
∈R),它与曲线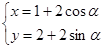 (
(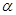 为参数)相交于两点A和B,则
为参数)相交于两点A和B,则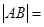 .
.