题目内容
已知函数f(x)的图象可由函数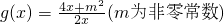 的图象向右平移两个单位而得到.
的图象向右平移两个单位而得到.
(1)写出函数f(x)的解析式;
(2)证明函数f(x)的图象关于直线y=x对称;
(3)问:是否存在集合M,当x∈M时,函数f(x)的最大值为2+m2,最小值为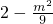 ;若存在,试求出一个集合M;若不存在,请说明理由.
;若存在,试求出一个集合M;若不存在,请说明理由.
(1)解:∵函数f(x)的图象可由函数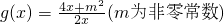 的图象向右平移两个单位而得到,
的图象向右平移两个单位而得到,
∴f(x)=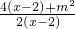 ;
;
(2)证明:令y=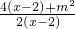 ,则y-2=
,则y-2=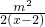
∴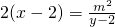
∴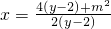
∴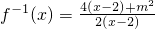
∴函数f(x)的图象关于直线y=x对称;
(3)解:f(x)=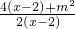 =2+
=2+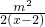
∵函数f(x)的最大值为2+m2,最小值为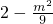
∴y=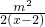 的最大值为m2,最小值为
的最大值为m2,最小值为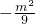
∴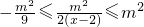
∴x≤ 或
或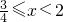 或x>2,
或x>2,
∴存在集合M={x|x≤ 或
或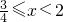 或x>2},当x∈M时,函数f(x)的最大值为2+m2,最小值为
或x>2},当x∈M时,函数f(x)的最大值为2+m2,最小值为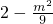 .
.
分析:(1)利用左加右减的平移规律,可得结论;
(2)证明函数f(x)的反函数是本身,即可得到结论;
(3)函数f(x)的最大值为2+m2,最小值为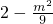 ,转化为y=
,转化为y=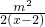 的最大值为m2,最小值为
的最大值为m2,最小值为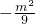 ,从而可得不等式,解不等式,即可得到结论.
,从而可得不等式,解不等式,即可得到结论.
点评:本题考查函数图象的平移,考查解不等式,考查学生分析解决问题的能力,属于中档题.
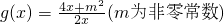 的图象向右平移两个单位而得到,
的图象向右平移两个单位而得到,∴f(x)=
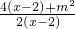 ;
;(2)证明:令y=
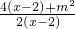 ,则y-2=
,则y-2=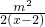
∴
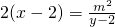
∴
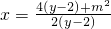
∴
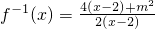
∴函数f(x)的图象关于直线y=x对称;
(3)解:f(x)=
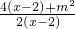 =2+
=2+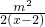
∵函数f(x)的最大值为2+m2,最小值为
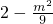
∴y=
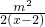 的最大值为m2,最小值为
的最大值为m2,最小值为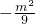
∴
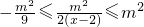
∴x≤
 或
或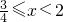 或x>2,
或x>2,∴存在集合M={x|x≤
 或
或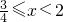 或x>2},当x∈M时,函数f(x)的最大值为2+m2,最小值为
或x>2},当x∈M时,函数f(x)的最大值为2+m2,最小值为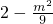 .
.分析:(1)利用左加右减的平移规律,可得结论;
(2)证明函数f(x)的反函数是本身,即可得到结论;
(3)函数f(x)的最大值为2+m2,最小值为
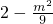 ,转化为y=
,转化为y=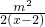 的最大值为m2,最小值为
的最大值为m2,最小值为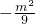 ,从而可得不等式,解不等式,即可得到结论.
,从而可得不等式,解不等式,即可得到结论.点评:本题考查函数图象的平移,考查解不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(