题目内容
(2012•天门模拟)已知函数f(x)的图象经过点(1,λ),且对任意x∈R,都有f(x+1)=f(x)+2.数列{an}满足a1=λ-2,2an+1=
(I)求f(n)(n∈N*)的表达式;
(II)设λ=3,求a1+a2+a3+…+a2n;
(III)若对任意n∈N*,总有anan+1<an+1an+2,求实数λ的取值范围.
|
(I)求f(n)(n∈N*)的表达式;
(II)设λ=3,求a1+a2+a3+…+a2n;
(III)若对任意n∈N*,总有anan+1<an+1an+2,求实数λ的取值范围.
分析:(I)记bn=f(n),由f(x+1)=f(x)+2知数列{bn}为首项为λ,公差为2的等差数列,从而求出bn.即f(n).
(II)要求a1+a2+a3+…+a2n即求(a1+a3+…+a2n-1)+(a2+a4+…+a2n)再将an的值分别代入即可.
(III)由于an的通项公式有三个,所以分n为奇数和偶数两种情况讨论,
当n为奇数且n≥3时,判断an+1an+2与anan+1=an+1(an+2-an大小得λ的范围,
当n为偶数时,判断an+1an+2与anan+1=an+1(an+2-an)的大小,并且求出λ>-2
(II)要求a1+a2+a3+…+a2n即求(a1+a3+…+a2n-1)+(a2+a4+…+a2n)再将an的值分别代入即可.
(III)由于an的通项公式有三个,所以分n为奇数和偶数两种情况讨论,
当n为奇数且n≥3时,判断an+1an+2与anan+1=an+1(an+2-an大小得λ的范围,
当n为偶数时,判断an+1an+2与anan+1=an+1(an+2-an)的大小,并且求出λ>-2
解答:解:(I)记bn=f(n),由f(x+1)=f(x)+2有bn+1-bn=2对任意n∈N*都成立,
又b1=f(1)=λ,所以数列{bn}为首项为λ,公差为2的等差数列,
故bn=2n+λ-2.即f(n)=2n+λ-2.
(II)由题设λ=3
若n为偶数,则an=2n-1;
若n为奇数且n≥3,则
an=f(an-1)=2an-1+λ-2=2•2n-2+λ-2=2n-1+λ-2=2n-1+1
又a1=λ-2=1,
即an=
a1+a2+a3+…+a2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)
=(20+22+…+22n-2+n-1)+(21+23+…+22n-1)
=(1+2+22+…+22n-1)+n-1
=22n+n-2
(III)当n为奇数且n≥3时,
an+1an+2-anan+1=an+1(an+2-an)=2n[2n+1+λ-2-(2n-1+λ-2)]
=3•22n-1>0;
当n为偶数时,
an+1an+2-anan+1=an+1(an+2-an)=(2n+λ-2)(2n+1-2n-1)]
=3•2n-1(2n+λ-2)
因为anan+1<an+1an+2,所以2n+λ-2>0,
∵n为偶数,∴n≥2,
∵2n+λ-2单增,∴4+λ-2>0
即λ>-2
故λ得取值范围为(-2,+∞).
又b1=f(1)=λ,所以数列{bn}为首项为λ,公差为2的等差数列,
故bn=2n+λ-2.即f(n)=2n+λ-2.
(II)由题设λ=3
若n为偶数,则an=2n-1;
若n为奇数且n≥3,则
an=f(an-1)=2an-1+λ-2=2•2n-2+λ-2=2n-1+λ-2=2n-1+1
又a1=λ-2=1,
即an=
|
a1+a2+a3+…+a2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)
=(20+22+…+22n-2+n-1)+(21+23+…+22n-1)
=(1+2+22+…+22n-1)+n-1
=22n+n-2
(III)当n为奇数且n≥3时,
an+1an+2-anan+1=an+1(an+2-an)=2n[2n+1+λ-2-(2n-1+λ-2)]
=3•22n-1>0;
当n为偶数时,
an+1an+2-anan+1=an+1(an+2-an)=(2n+λ-2)(2n+1-2n-1)]
=3•2n-1(2n+λ-2)
因为anan+1<an+1an+2,所以2n+λ-2>0,
∵n为偶数,∴n≥2,
∵2n+λ-2单增,∴4+λ-2>0
即λ>-2
故λ得取值范围为(-2,+∞).
点评:此题考查等差数列的定义,及如何构造等差数列是解此题的关键.数列求和中注意要分n的奇偶性进行讨论.

练习册系列答案
相关题目
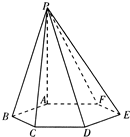 (2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )
(2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )