题目内容
(2011•济南二模)已知函数f(x)=plnx+(p-1)x2+1.
(1)讨论函数f(x)的单调性;
(2)当P=1时,f(x)≤kx恒成立,求实数k的取值范围;
(3)证明:1n(n+1)<1+
+
+…+
(n∈N+).
(1)讨论函数f(x)的单调性;
(2)当P=1时,f(x)≤kx恒成立,求实数k的取值范围;
(3)证明:1n(n+1)<1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
分析:(1)利用导数来讨论函数的单调性即可,具体的步骤是:(1)确定 f(x)的定义域;(2)求导数fˊ(x);(3)在函数 的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定 的单调区间.若在函数式中含字母系数,往往要分类讨论.(2)当P=1时,f(x)≤kx恒成立,分离参数等价于k≥
,利用导数求函数h(x)=
的最大值即可求得实数k的取值范围;(3)由(2)知,当k=1时,有f(x)≤x,当x>1时,f(x)<x,即lnx<x-1,令x=
,则得到ln
<
,利用导数的运算法则进行化简,然后再相加,即可证得结论.
| 1+lnx |
| x |
| 1+lnx |
| x |
| n+1 |
| n |
| n+1 |
| n |
| 1 |
| n |
解答:解:(1)f(x)的定义域为(0,+∞),f′(x)=
+2(p-1)x=
,
当p>1时,f′(x)>0,故f(x)在(0,+∞)上单调递增;
当p≤0时,f′(x)<0,故f(x)在(0,+∞)上单调递减;
当0<p<1时,令f′(x)=0,解得x=
.
则当x∈(0,
)时,f′(x)>0;x∈(
,+∞)时,f′(x)<0,
故f(x)在(0,
)上单调递增,在(
,+∞)上单调递减;
(2)∵x>0,
∴当p=1时,f(x)≤kx恒成立?1+lnx≤kx?k≥
,
令h(x)=
,则k≥h(x)max,
∵h′(x)=
=0,得x=1,
且当x∈(0,1),h′(x)>0;当x∈(1,+∞),h′(x)<0;
所以h(x)在0,1)上递增,在(1,+∞)上递减,
所以h(x)max=h(1)=1,
故k≥1.
(3)由(2)知,当k=1时,有f(x)≤x,当x>1时,f(x)<x,即lnx<x-1,
∴令x=
,则ln
<
,即ln(n+1)-lnn<
,
∴ln2-ln1<1,ln3-ln2<
,…,ln(n+1)-lnn<
相加得1n(n+1)<1+
+
+…+
.
| p |
| x |
| 2(p-1)x2+p |
| x |
当p>1时,f′(x)>0,故f(x)在(0,+∞)上单调递增;
当p≤0时,f′(x)<0,故f(x)在(0,+∞)上单调递减;
当0<p<1时,令f′(x)=0,解得x=
-
|
则当x∈(0,
-
|
-
|
故f(x)在(0,
-
|
-
|
(2)∵x>0,
∴当p=1时,f(x)≤kx恒成立?1+lnx≤kx?k≥
| 1+lnx |
| x |
令h(x)=
| 1+lnx |
| x |
∵h′(x)=
| -lnx |
| x2 |
且当x∈(0,1),h′(x)>0;当x∈(1,+∞),h′(x)<0;
所以h(x)在0,1)上递增,在(1,+∞)上递减,
所以h(x)max=h(1)=1,
故k≥1.
(3)由(2)知,当k=1时,有f(x)≤x,当x>1时,f(x)<x,即lnx<x-1,
∴令x=
| n+1 |
| n |
| n+1 |
| n |
| 1 |
| n |
| 1 |
| n |
∴ln2-ln1<1,ln3-ln2<
| 1 |
| 2 |
| 1 |
| n |
相加得1n(n+1)<1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
点评:此题是个难题.本题主要考查导数的概念、利用导数研究函数的单调性、利用函数的单调性证明不等式和利用导数研究函数性质的能力,考查分类讨论思想、数形结合思想和等价变换思想.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
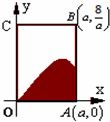 (2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
(2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为