题目内容
(2011•济南二模)在数列{an}中,a1=1,并且对于任意n∈N*,都有an+1=
.
(1)证明数列{
}为等差数列,并求{an}的通项公式;
(2)设数列{anan+1}的前n项和为Tn,求使得Tn>
的最小正整数n.
| an |
| 2an+1 |
(1)证明数列{
| 1 |
| an |
(2)设数列{anan+1}的前n项和为Tn,求使得Tn>
| 1000 |
| 2011 |
分析:(1)
=1,an+1=
,所以
-
=2,由此能求出{an}的通项公式.
(2)因为anan+1=
=
(
-
),所以Tn=a1a2+a2a3+…+anan+1=
[(1-
)+(
-
)+…+(
-
)]=
,由Tn>
,得最小正整数n为91.
| 1 |
| a1 |
| an |
| 2an+1 |
| 1 |
| an+1 |
| 1 |
| an |
(2)因为anan+1=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
| 1000 |
| 2011 |
解答:解:(1)
=1,
因为an+1=
,所以
-
=2,
∴数列{
}是首项为1,公差为2的等差数列,(4分)
∴
=2n-1,
从而an=
.(6分)
(2)因为anan+1=
=
(
-
)(8分)
所以Tn=a1a2+a2a3+…+anan+1
=
[(1-
)+(
-
)+…+(
-
)]
=
(10分)
由Tn>
,得n>
,最小正整数n为91.(12分)
| 1 |
| a1 |
因为an+1=
| an |
| 2an+1 |
| 1 |
| an+1 |
| 1 |
| an |
∴数列{
| 1 |
| an |
∴
| 1 |
| an |
从而an=
| 1 |
| 2n-1 |
(2)因为anan+1=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=a1a2+a2a3+…+anan+1
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
由Tn>
| 1000 |
| 2011 |
| 1000 |
| 11 |
点评:本题考查数列的通项公式的求法和前n项和的求法,解题时要注意构造成法和裂项求和法的合理运用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
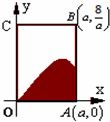 (2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
(2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为