题目内容
如果函数f(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数,那么实数a的取值范围是______.
[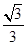 ,1)
,1)
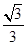 ,1)
,1)函数y=ax(ax-3a2-1)(a>0且a≠1)可以看做是关于ax的二次函数.
若a>1,则y=ax是增函数,原函数在区间[0,+∞)上是增函数,则要求对称轴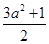 ≤0,矛盾;
≤0,矛盾;
若0<a<1,则y=ax是减函数,原函数在区间[0,+∞)上是增函数,则要求当t=ax(0<t≤1)时,y=t2-(3a2+1)t在t∈(0,1]上为减函数,即对称轴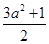 ≥1,
≥1,
所以a2≥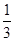 .所以实数a的取值范围是[
.所以实数a的取值范围是[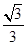 ,1).
,1).
若a>1,则y=ax是增函数,原函数在区间[0,+∞)上是增函数,则要求对称轴
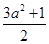 ≤0,矛盾;
≤0,矛盾;若0<a<1,则y=ax是减函数,原函数在区间[0,+∞)上是增函数,则要求当t=ax(0<t≤1)时,y=t2-(3a2+1)t在t∈(0,1]上为减函数,即对称轴
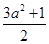 ≥1,
≥1,所以a2≥
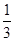 .所以实数a的取值范围是[
.所以实数a的取值范围是[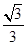 ,1).
,1).
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
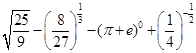 ; ②
; ②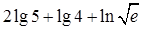 .
. 有两个不等实根,则实数
有两个不等实根,则实数 的取值范围是( )
的取值范围是( )



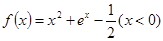 与
与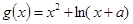 图象上存在关于
图象上存在关于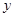 轴对称的点,则
轴对称的点,则 的取值范围是( )
的取值范围是( )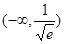
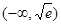
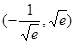
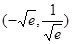
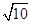 ,则
,则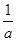 +
+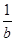 =( )
=( )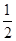
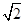
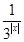 .
.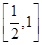 恒成立,求m的取值范围.
恒成立,求m的取值范围. ,
, ,则
,则 ________.
________.