题目内容
已知函数f(x)＝3x－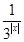
.
(1)若f(x)＝2，求x的值；
(2)判断x>0时，f(x)的单调性；
(3)若3tf(2t)＋mf(t)≥0对于t∈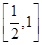
恒成立，求m的取值范围．
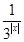.(1)若f(x)＝2，求x的值；
(2)判断x>0时，f(x)的单调性；
(3)若3tf(2t)＋mf(t)≥0对于t∈
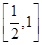恒成立，求m的取值范围．（1）log3(1＋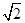
)
（2）f(x)＝3x－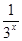
在(0，＋∞)上单调递增
（3）[－4，＋∞)
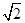)（2）f(x)＝3x－
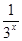在(0，＋∞)上单调递增（3）[－4，＋∞)
解：(1)当x≤0时，f(x)＝3x－3x＝0，
∴f(x)＝2无解．
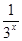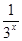当x>0时，f(x)＝3x－，令3x－＝2.
∴(3x)2－2·3x－1＝0，解得3x＝1±.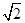
∵3x>0，∴3x＝1＋.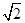
∴x＝log3(1＋)．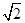
(2)∵y＝3x在(0，＋∞)上单调递增，
y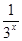＝在(0，＋∞)上单调递减，
∴f(x)＝3x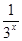－在(0，＋∞)上单调递增．
(3)∵t∈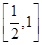，∴f(t)＝3t－
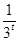>0.
∴3tf(2t)＋mf(t)≥0化为
3t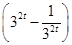
＋m
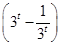≥0，
即3t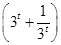
＋m≥0，即m≥－32t－1.
令g(t)＝－32t－1，则g(t)在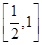上递减，∴g(x)max＝－4.
∴所求实数m的取值范围是[－4，＋∞)．
∴f(x)＝2无解．
当x>0时，f(x)＝3x－
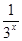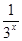，令3x－＝2.∴(3x)2－2·3x－1＝0，解得3x＝1±
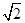.∵3x>0，∴3x＝1＋
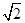.∴x＝log3(1＋
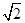)．(2)∵y＝3x在(0，＋∞)上单调递增，
y＝
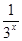在(0，＋∞)上单调递减，∴f(x)＝3x－
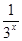在(0，＋∞)上单调递增．(3)∵t∈
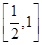，∴f(t)＝3t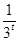－>0.∴3tf(2t)＋mf(t)≥0化为
3t
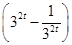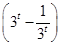＋m≥0，即3t
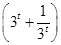＋m≥0，即m≥－32t－1.令g(t)＝－32t－1，则g(t)在
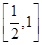上递减，∴g(x)max＝－4.∴所求实数m的取值范围是[－4，＋∞)．
练习册系列答案
相关题目
，则
.
)－1.2，则a，b，c的大小关系为( )
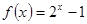的反函数为________.
，
，
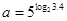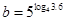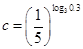，则( )