题目内容
已知各项都不相等的等差数列 的前6项和为60,且
的前6项和为60,且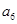 为
为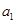 和
和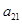 的等比中项.
的等比中项.
(1) 求数列 的通项公式;
的通项公式;
(2) 若数列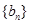 满足
满足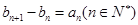 ,且
,且 ,求数列
,求数列 的前
的前 项和
项和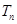 .
.
(1) 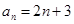 ;(2)
;(2)  .
.
解析试题分析:(1) 求数列 的通项公式,因为是等差数列,故只需求出
的通项公式,因为是等差数列,故只需求出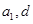 即可,由已知前6项和为60,且
即可,由已知前6项和为60,且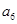 为
为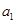 和
和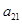 的等比中项,可得
的等比中项,可得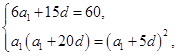 ,解方程组得
,解方程组得 ,从而可得数列
,从而可得数列 的通项公式;(2) 求数列
的通项公式;(2) 求数列 的前
的前 项和
项和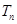 ,首先求出数列
,首先求出数列 的通项公式,由已知数列
的通项公式,由已知数列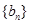 满足
满足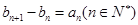 ,且
,且 ,可用迭代法(或叠加法)求出数列
,可用迭代法(或叠加法)求出数列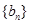 的通项公式
的通项公式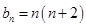 ,从而得
,从而得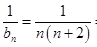 ,求数列
,求数列 的前
的前 项和
项和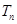 ,可用拆项相消法求和.
,可用拆项相消法求和.
试题解析:(1) 设等差数列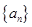 的公差为
的公差为 (
( ),
),
则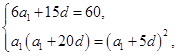 2分
2分
解得 4分
4分
∴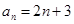 . 5分
. 5分
(2) 由 ,
,
∴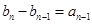
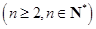 , 6分
, 6分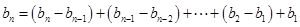
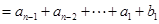
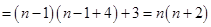 .
.
∴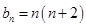
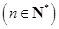 . 8分
. 8分
∴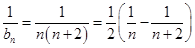 10分
10分
 . 12分
. 12分
考点:等差数列的通项公式,数列求和.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
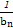 }的前n项和Tn.
}的前n项和Tn.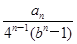 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3. 的前
的前 项和为
项和为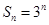 ,数列
,数列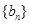 满足:
满足: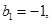
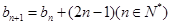 。
。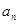 ;
;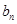 ;(3)若
;(3)若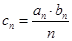 ,求数列
,求数列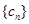 的前
的前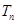 .
. 的各项均为正数,
的各项均为正数,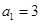 ,前
,前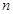 项和为
项和为 ,
,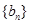 为等比数列,
为等比数列, 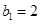 ,且
,且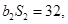
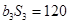 .
.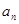 与
与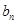 ;
;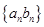 的前
的前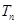 .
. 满足:
满足: .
. 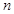 项和
项和 ;
;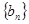 的前
的前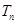 ,且
,且 ,求
,求 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且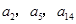 分别是等比数列{
分别是等比数列{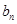 }的b2,b3,b4.
}的b2,b3,b4.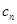 }对任意自然数n均有
}对任意自然数n均有 成立,求
成立,求 的值.
的值. 中,
中,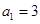 ,
, ,
,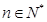 .
. 是等比数列,并求数列
是等比数列,并求数列 且
且 ,
,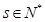 ,求证:使得
,求证:使得 ,
,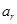 ,
, 成等差数列的点列
成等差数列的点列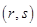 在某一直线上.
在某一直线上.