题目内容
已知数列 中,
中,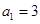 ,
, ,
,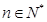 .
.
(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)在数列 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若 且
且 ,
,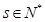 ,求证:使得
,求证:使得 ,
,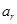 ,
, 成等差数列的点列
成等差数列的点列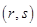 在某一直线上.
在某一直线上.
(1)详见解析;(2)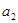 ,
,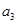 ,
, 成等差数列;(3)详见解析.
成等差数列;(3)详见解析.
解析试题分析:(1)证明一个数列为等比或等差数列,一般都是从定义入手,本小题首先需要将已知条件 变形为
变形为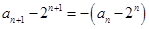 ,由于
,由于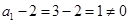 ,则
,则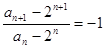 (常数),然后根据等比数列的定义可知数列
(常数),然后根据等比数列的定义可知数列 是以
是以 为首项,公比为
为首项,公比为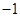 的等比数列,即
的等比数列,即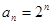
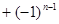 (
( );
);
(2)本小题首先假设在数列 中存在连续三项
中存在连续三项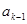 ,
, ,
,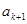 (
( ,
,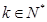 )成等差数列,则
)成等差数列,则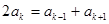 ,代入通项公式可得
,代入通项公式可得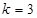 ,即
,即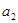 ,
,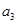 ,
, 成等差数列.
成等差数列.
(3)本小题首先根据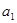 ,
,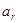 ,
,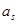 成等差数列,则
成等差数列,则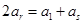 ,于是可得
,于是可得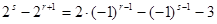 ,然后通过不定方程的分类讨论可得结论
,然后通过不定方程的分类讨论可得结论
试题解析:(1)将已知条件 变形为
变形为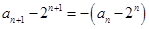 1分
1分
由于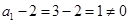 ,则
,则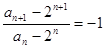 (常数) 3分
(常数) 3分
即数列 是以
是以 为首项,公比为
为首项,公比为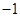 的等比数列 4分
的等比数列 4分
所以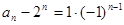
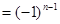 ,即
,即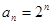
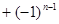 (
( )。 5分
)。 5分
(2)假设在数列 中存在连续三项成等差数列,
中存在连续三项成等差数列,
不妨设连续的三项依次为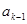 ,
, ,
,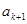 (
( ,
,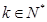 ),
),
由题意得,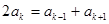 ,
,
将 ,
,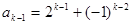 ,
,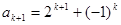 代入上式得 7分
代入上式得 7分 8分
8分
化简得,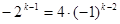 ,即
,即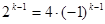 ,得
,得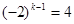 ,解得
,解得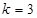
所以,存在满足条件的连续三项为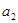 ,
,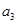 ,
, 成等差数列。 10分
成等差数列。 10分
(3)若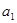 ,
,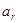 ,
,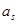 成等差数列,则
成等差数列,则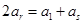
即 ,变形得
,变形得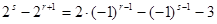 11分
11分
由于若 ,
,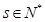 且
且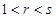 ,下面对
,下面对 、
、 进行讨论:
进行讨论:
① 若 ,
, 均为偶数,则
均为偶数,则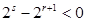 ,解得
,解得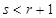 ,与
,与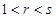 矛盾,舍去;
矛盾,舍去;
② 若

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 的前6项和为60,且
的前6项和为60,且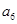 为
为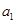 和
和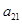 的等比中项.
的等比中项.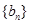 满足
满足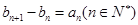 ,且
,且 ,求数列
,求数列 的前
的前 项和
项和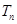 .
.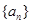 的前n项和为
的前n项和为 ,
,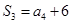 ,且
,且 成等比数列.
成等比数列.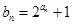 ,求数列
,求数列 的前n项和.
的前n项和.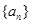 的各项均为正数,
的各项均为正数,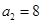 ,
,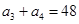 .
.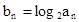 .证明:
.证明: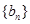 为等差数列,并求
为等差数列,并求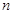 项和
项和 .
. ,
, 满足
满足 ,
, ,且对任意的正整数
,且对任意的正整数 ,
, 和
和 均成等比数列.
均成等比数列. 、
、 的值;
的值; 和
和 均成等比数列;
均成等比数列; ,使得
,使得 恒成立?证明你的结论.
恒成立?证明你的结论.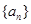 的前
的前 项和为
项和为 ,且
,且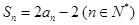 ,数列
,数列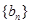 满足
满足 ,且
,且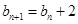 .
. 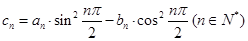 ,求数列
,求数列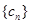 的前
的前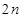 项和
项和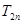 .
. 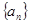 中,
中,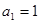 ,公差
,公差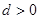 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列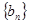 的第2项,第3项,第4项.
的第2项,第3项,第4项.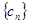 对任意自然数均有
对任意自然数均有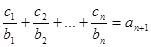 成立,求
成立,求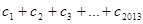 的值.
的值.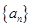 的前
的前 项和为
项和为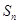 ,若
,若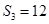 ,且
,且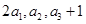 成等比数列.
成等比数列.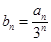 的前
的前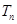 ,求
,求 的前
的前 项和为
项和为 .且
.且 .
. ,数列
,数列 满足:
满足:

 ,求数列
,求数列 的前
的前 项和
项和 .
.