题目内容
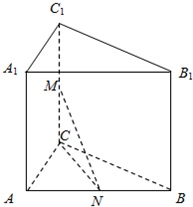如图，已知直三棱柱ABC-A1B1C1中，AC=BC=2，M、N分别是棱CC1、AB的中点．求证：平面MCN⊥平面ABB1A1．分析：利用直三棱柱ABC-A1B1C1中，CC1⊥底面ABC，推出AB⊥CC1，证明AB⊥CN，推出AB⊥平面MCN，然后证明平面MCN⊥平面ABB1A1
解答：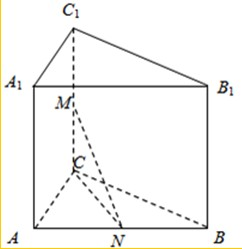
证明：在直三棱柱ABC-A1B1C1中，
CC1⊥底面ABC…（2分）
因为AB?平面ABC，
所以AB⊥CC1 …（5分）
又因为AC=BC=2，
N是AB中点，
所以AB⊥CN．…（7分）
由于CC1∩CN=C且CC1、CN?平面MCN，
所以AB⊥平面MCN …（10分）
又因为AB?平面ABB1A1，
所以 平面MCN⊥平面ABB1A1．…（12分）
证明：在直三棱柱ABC-A1B1C1中，CC1⊥底面ABC…（2分）
因为AB?平面ABC，
所以AB⊥CC1 …（5分）
又因为AC=BC=2，
N是AB中点，
所以AB⊥CN．…（7分）
由于CC1∩CN=C且CC1、CN?平面MCN，
所以AB⊥平面MCN …（10分）
又因为AB?平面ABB1A1，
所以 平面MCN⊥平面ABB1A1．…（12分）
点评：本题考查通过直线与直线垂直，证明平面与平面垂直的证明方法，考查平面与平面垂直的判断，考查逻辑推理能力．
练习册系列答案
相关题目
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CC1、AB中点．
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=BC=2，AA1=4．
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4，E、F分别是棱CC1、AB中点．
如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．
（2010•莒县模拟）如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CCl、AB中点．