题目内容
如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．（Ⅰ）求异面直线AB和C1D所成的角（用反三角函数表示）；
（Ⅱ）若E为AB上一点，试确定点E在AB上的位置，使得A1E⊥C1D；
（Ⅲ）在（Ⅱ）的条件下，求点D到平面B1C1E的距离．
分析：（Ⅰ）法一：利用平行四边形的性质把其中一条平移及异面直线所成的角的定义、三角形中的三角函数的计算即可求出；
法二：建立空间直角坐标系，利用异面直线的方向向量所成的角即可求出异面直线所成的角；
（Ⅱ）法一：过C1作C1M⊥A1B1，垂足为M，则M为A1B1的中点，且C1M⊥平面AA1B1B．连接DM，利用三垂线定理即可找出点E的位置；
法二：过E作EN⊥AC，垂足为N，则EN⊥平面AA1C1C，连接A1N．利用三垂线定理即可证明；
法三：建立空间直角坐标系，利用
⊥
?
•
=0即可求出；
（Ⅲ）法一：利用线面、面面垂直的判定和性质即可求出；
法二：利用“等积变形”即可求出．
法二：建立空间直角坐标系，利用异面直线的方向向量所成的角即可求出异面直线所成的角；
（Ⅱ）法一：过C1作C1M⊥A1B1，垂足为M，则M为A1B1的中点，且C1M⊥平面AA1B1B．连接DM，利用三垂线定理即可找出点E的位置；
法二：过E作EN⊥AC，垂足为N，则EN⊥平面AA1C1C，连接A1N．利用三垂线定理即可证明；
法三：建立空间直角坐标系，利用
| A1E |
| C1D |
| A1E |
| C1D |
（Ⅲ）法一：利用线面、面面垂直的判定和性质即可求出；
法二：利用“等积变形”即可求出．
解答：（Ⅰ）法一：取CC1的中点F，连接AF，BF，则AF∥C1D．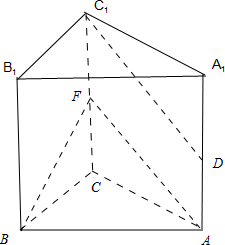
∴∠BAF为异面直线AB与C1D所成的角或其补角．
∵△ABC为等腰直角三角形，AC=2，∴AB=2
．
又∵CC1=2，∴AF=BF=
．
∵cos∠BAF=
=
，
∴∠BAF=arccos
，
即异面直线AB与C1D所成的角为arccos
．
法二：以C为坐标原点，CB，CA，CC1分别为x轴，y轴，z轴建立空间直角坐标系，
则A（0，2，0），B（2，0，0），
C1（0，0，2），D（0，2，1），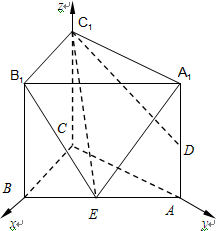
∴
=（2，-2，0），
=（0，2，-1）．由于异面直线AB与C1D所成的角
为向量
与
的夹角或其补角．设
与
夹角为θ，
则cosθ=
=-
，θ=π-arccos
，
即异面直线AB与C1D所成的角为arccosθ．
（Ⅱ）法一：过C1作C1M⊥A1B1，垂足为M，则M为A1B1的中点，且C1M⊥平面AA1B1B．连接DM．
∴DM即为C1D在平面AA1B1B上的射影．要使得A1E⊥C1D，由三垂线定理知，只要A1E⊥DM．
∵AA1=2，AB=2
，由计算知，E为AB的中点．
法二：过E作EN⊥AC，垂足为N，则EN⊥平面AA1C1C．
连接A1N．∴A1N即为A1E在平面AA1C1C上的射影．要使得A1E⊥C1D，由三垂线定理知，只要A1N⊥C1D．
∵四边形AA1C1C为正方形，∴N为AC的中点，∴E点为AB的中点．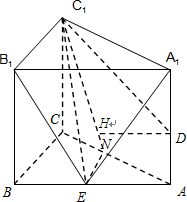
法三：以C为坐标原点，CB，CA，CC1分别为x轴，y轴，z轴建立空间直角坐标系，
则A1（0，2，2），B（2，0，0），A（0，2，0），
C1（0，0，2），D（0，2，1），
设E点的坐标为（x，y，0），
要使得A1E⊥C1D，
只要
•
=0，∵
=（x，y-2，-2），
=（0，2，-1），y=1．
又∵点E在AB上，∴
∥
，
=(x，y-2，0)，
=(2，-2，0)．
∴x=1．
∴E（1，1，0）．
∴E点为AB的中点．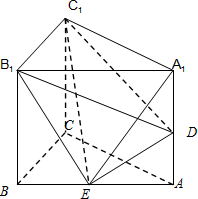
（Ⅲ）法一：取AC中点N，连接EN，C1N，
则EN∥B1C1．∵B1C1⊥平面AA1C1C，∴面B1C1NE⊥平面AA1C1C．
过点D作DH⊥C1N，垂足为H，则DH⊥平面B1C1NE，
∴DH的长度即为点D到平面B1C1E的距离．
在正方形AA1C1C中，由计算知DH=
，即点D到平面B1C1E的 距离
．
法二：连接DE，DB1．
在三棱锥D-B1C1E中，点C1到平面DB1E的距离
=
，B1E=
，DE=
，
又B1E⊥DE，∴△DB1E的面积=
×
×
=
，
∴三棱锥C1-DB1E的体积为=
×
×
=1．
设点D到平面B1C1E的距离为d，在△B1C1E中，B1C1=2，B1E=C1E=
，
∴△B1C1E的面积=
×2×
=
．由
×d×
=1，
得d=
，即点D到平面B1C1E的距离
．
∴∠BAF为异面直线AB与C1D所成的角或其补角．
∵△ABC为等腰直角三角形，AC=2，∴AB=2
| 2 |
又∵CC1=2，∴AF=BF=
| 5 |
∵cos∠BAF=
| ||
|
| ||
| 5 |
∴∠BAF=arccos
| ||
| 5 |
即异面直线AB与C1D所成的角为arccos
| ||
| 5 |
法二：以C为坐标原点，CB，CA，CC1分别为x轴，y轴，z轴建立空间直角坐标系，
则A（0，2，0），B（2，0，0），
C1（0，0，2），D（0，2，1），
∴
| AB |
| C1D |
为向量
| AB |
| C1D |
| AB |
| C1D |
则cosθ=
| -4 | ||||
2
|
| ||
| 5 |
| ||
| 5 |
即异面直线AB与C1D所成的角为arccosθ．
（Ⅱ）法一：过C1作C1M⊥A1B1，垂足为M，则M为A1B1的中点，且C1M⊥平面AA1B1B．连接DM．
∴DM即为C1D在平面AA1B1B上的射影．要使得A1E⊥C1D，由三垂线定理知，只要A1E⊥DM．
∵AA1=2，AB=2
| 2 |
法二：过E作EN⊥AC，垂足为N，则EN⊥平面AA1C1C．
连接A1N．∴A1N即为A1E在平面AA1C1C上的射影．要使得A1E⊥C1D，由三垂线定理知，只要A1N⊥C1D．
∵四边形AA1C1C为正方形，∴N为AC的中点，∴E点为AB的中点．
法三：以C为坐标原点，CB，CA，CC1分别为x轴，y轴，z轴建立空间直角坐标系，
则A1（0，2，2），B（2，0，0），A（0，2，0），
C1（0，0，2），D（0，2，1），
设E点的坐标为（x，y，0），
要使得A1E⊥C1D，
只要
| A1E |
| C1D |
| A1E |
| C1D |
又∵点E在AB上，∴
| AE |
| AB |
| AE |
| AB |
∴x=1．
∴E（1，1，0）．
∴E点为AB的中点．
（Ⅲ）法一：取AC中点N，连接EN，C1N，
则EN∥B1C1．∵B1C1⊥平面AA1C1C，∴面B1C1NE⊥平面AA1C1C．
过点D作DH⊥C1N，垂足为H，则DH⊥平面B1C1NE，
∴DH的长度即为点D到平面B1C1E的距离．
在正方形AA1C1C中，由计算知DH=
3
| ||
| 5 |
3
| ||
| 5 |
法二：连接DE，DB1．
在三棱锥D-B1C1E中，点C1到平面DB1E的距离
=
| 2 |
| 6 |
| 3 |
又B1E⊥DE，∴△DB1E的面积=
| 1 |
| 2 |
| 6 |
| 2 |
3
| ||
| 2 |
∴三棱锥C1-DB1E的体积为=
| 1 |
| 3 |
3
| ||
| 2 |
| 2 |
设点D到平面B1C1E的距离为d，在△B1C1E中，B1C1=2，B1E=C1E=
| 6 |
∴△B1C1E的面积=
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 3 |
| 5 |
得d=
3
| ||
| 5 |
3
| ||
| 5 |
点评：本题综合考查了空间中的空间角、线面位置关系、空间距离，熟练掌握平行四边形的性质、异面直线所成的角的定义、三角形中的三角函数的计算、三垂线定理、通过建立空间直角坐标系利用直线的方向向量及平面的法向量的夹角、
⊥
?
•
=0、线面与面面垂直的判定和性质、“等积变形”是解题的关键．
| A1E |
| C1D |
| A1E |
| C1D |
练习册系列答案
相关题目
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CC1、AB中点．
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=BC=2，AA1=4．
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4，E、F分别是棱CC1、AB中点．
（2010•莒县模拟）如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CCl、AB中点．