题目内容
有4个编号分别为1、2、3、4的小球全部放入同样编号为1、2、3、4的4个盒子中,每个盒子只能放一个球,则有且只有一个小球和盒子编号相同的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:总的方法为4的全排列,其中有且只有一个小球和盒子编号相同的有8种,由概率公式可得.
解答:
解:4个球放到4个盒子共有
=24种方法,
其中有且只有一个小球和盒子编号相同的有
•2=8种,
(不妨设1号球放到了1号盒,则另外3个球的放置只有342和423两种)
∴所求概率为P=
=
故选:B
| A | 4 4 |
其中有且只有一个小球和盒子编号相同的有
| C | 1 4 |
(不妨设1号球放到了1号盒,则另外3个球的放置只有342和423两种)
∴所求概率为P=
| 8 |
| 24 |
| 1 |
| 3 |
故选:B
点评:本题考查古典概型及其概率公式,属基础题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
若数列{an}满足
-
=d(n∈Nn,d为常数),则称数列{an}为“调和数列”.已知数列{
}为“调和数列”,且x1+x2+…+x20=200,则x3•x18的最大值为( )
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| xn |
| A、50 | B、100 |
| C、150 | D、200 |
设变量x,y满足约束条件
,则目标函数z=2x+3y的最大值为( )
|
| A、22 | B、20 | C、5 | D、4 |
数列{an}满足a1=2,an+1=-
,则a2008=( )
| 1 |
| an+1 |
| A、2 | ||
B、-
| ||
C、-
| ||
| D、1 |
设有直线a,b,c,d及平面α,β,下列条件能推出α∥β的是( )
| A、a?α,b?β,a∥b,c?α,d?β,c∥d |
| B、a?α,b?β,a∥β,b∥α |
| C、a⊥α,b⊥β,a∥b |
| D、平面α内有三个不共线的点到β距离相等 |




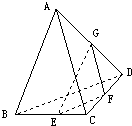 E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )
E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )