题目内容
8.已知f(n)=${∫}_{0}^{\frac{π}{n}}$sin(nx)dx,若对于?∈R,f(1)+f(2)+…+f(n)<|x+3|+|x-1|恒成立,则正整数n的最大值为3.分析 先根据定积分计算出f(n),再根据绝对值的几何意义求出|x+3|+|x-1|的最小值为4,继而得到n的最大值.
解答 解:f(n)=${∫}_{0}^{\frac{π}{n}}$sin(nx)dx=-$\frac{1}{n}$cosnx${|}_{0}^{\frac{π}{n}}$=-$\frac{1}{n}$(cosπ-cos0)=$\frac{2}{n}$,
根据绝对值的几何意义,得到|x+3|+|x-1|≥4,
∵对于?∈R,f(1)+f(2)+…+f(n)<|x+3|+|x-1|恒成立,
∴$\frac{2}{1}$+$\frac{2}{2}$+$\frac{2}{3}$+$\frac{2}{4}$+…+$\frac{2}{n}$=3+$\frac{2}{3}$+$\frac{2}{4}$++…+$\frac{2}{n}$<4,
∴正整数n的最大值为3,
故答案为:3.
点评 本题考查了定积分的计算以及绝对值的几何意义,以及函数恒成立的问题,属于中档题.

练习册系列答案
相关题目
3.设平面区域D是由双曲线y2-$\frac{{x}^{2}}{4}$=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形区域(含边界),若点(x,y)∈D,则$\frac{2y-x+1}{x+1}$的取值范围是( )
| A. | [-1,$\frac{1}{3}$] | B. | [-1,1] | C. | [0,$\frac{1}{3}$] | D. | [0,$\frac{4}{3}$] |
13.函数f(x)=ln(x+2)+cosx的图象大致为( )
| A. |  | B. |  | C. |  | D. | 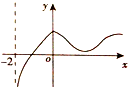 |
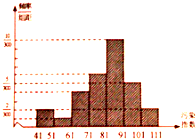 如图是某市2014年11月份30天的空气污染指数的频率分布直方图.根据国家标准,污染指数在区间[0,51)内,空气质量为优;在区间[51,101)内,空气质量为良;在区间[101,151)内,空气质量为轻微污染;…,由此可知该市11月份空气质量为优或良的天数有28天.
如图是某市2014年11月份30天的空气污染指数的频率分布直方图.根据国家标准,污染指数在区间[0,51)内,空气质量为优;在区间[51,101)内,空气质量为良;在区间[101,151)内,空气质量为轻微污染;…,由此可知该市11月份空气质量为优或良的天数有28天.