题目内容
【题目】已知函数![]()
![]() 且
且![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求证:
时,求证:![]() ;
;
(3)讨论函数![]() 的极值.
的极值.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析;(Ⅲ)详见解析.
;(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
(I)求得切点坐标和斜率,由此求得切线方程.(II)将原不等式转化为![]() 成立,构造函数
成立,构造函数![]() ,利用导数求得
,利用导数求得![]() 的最大值为零,由此证得不等式成立.(III)对
的最大值为零,由此证得不等式成立.(III)对![]() 求导后,对
求导后,对![]() 分成
分成![]() 两类,结合函数的单调区间,讨论得出函数的极值.
两类,结合函数的单调区间,讨论得出函数的极值.
解:(Ⅰ)当![]() 时,
时,![]() .所以
.所以![]() .
.
因为![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)当![]() 时,
时,![]() .
.
函数![]() 的定义域为
的定义域为![]() .
.
不等式![]() 成立
成立![]()
![]() 成立
成立![]()
![]() 成立.
成立.
设![]()
![]() ,
,
则![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
| + |
| - |
| ↗ | 极大值 | ↘ |
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
(Ⅲ)求导得![]() . 令
. 令![]() ,因为
,因为![]() 可得
可得![]() .
.
当![]() 时,
时,![]() 的定义域为
的定义域为![]() .当
.当![]() 变化时,
变化时,![]() ,
,![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
| + |
| - |
| ↗ | 极大值 | ↘ |
此时![]() 有极大值
有极大值![]() ,无极小值.
,无极小值.
当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,当
,当![]() 变化时,
变化时,![]() ,
,![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
| - |
| + |
| ↘ | 极小值 | ↗ |
此时![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.

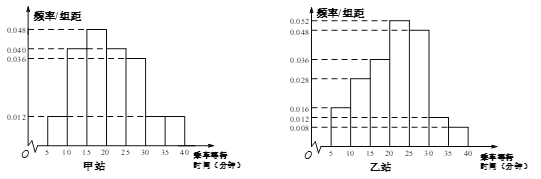
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了200名用户,得到用户的满意度评分,现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 |
|
|
|
|
|
频数 | 12 | 28 | 68 |
| 40 |
频率 | 0.06 |
| 0.34 |
| 0.2 |
(1)求表格中的![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计用户的满意度评分的平均数;
(3)若从这200名用户中随机抽取50人,估计满意度评分高于6分的人数为多少?
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数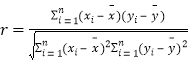 ,
,
回归方程![]() 中,
中,![]()
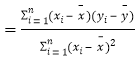 ,
,![]() .
.