题目内容
【题目】如图，
，
是通过某城市开发区中心O的两条南北和东西走向的街道，链接M，N两地之间的铁路是圆心在上的一段圆弧，若点M在O正北方向，且
，点N到，距离分别为4km和5km．
建立适当的坐标系，求铁路线所在圆弧的方程；
若该城市的某中学拟在O点正东方向选址建分校，考虑环境问题，要求校址到点O的距离大于4km，并且铁路线上任意一点到校址的距离不能少于
，求该校址距离点O的最近距离．
注：校址视为一个点
【答案】(1)
(2)距O最近6km的地方．
【解析】
建立坐标系，利用圆心在弦的垂直平分线上求圆心坐标，再求半径，进而写出圆的方程．
据条件列出不等式，运用函数单调性解决恒成立问题.
解：分别以
、
为x轴，y轴建立如图坐标系．
据题意得
，
，
，
MN中点为
，
线段MN的垂直平分线方程为：
，
故圆心A的坐标为
，
半径
．
弧MN的方程为：
设校址选在
，
对
恒成立．
即
，对恒成立
整理得：
，对恒成立
令
．
，
，
在
上为减函数．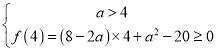
，
解得
，
即校址选在距O最近6km的地方．
练习册系列答案
相关题目
