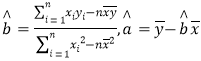题目内容
【题目】已知等差数列{an}满足a3＝2，前3项和为S3＝
.
(1)求{an}的通项公式；
(2)设等比数列{bn}满足b1＝a1，b4＝a15，求{bn}的前n项和Tn.
【答案】(1) 
;(2) 
.
【解析】试题分析:(1)根据等差数列的基本量运算解出
和
,代入公式算出等差数列
的通项公式;(2)计算出等比数列的首项和公比,代入求和公式计算.
试题解析:
(1)设{an}的公差为d，由已知得
解得a1＝1，d＝
，
故{an}的通项公式an＝1＋
，即an＝
.
(2)由(1)得b1＝1，b4＝a15＝
＝8.
设{bn}的公比为q，则q3＝
＝8，从而q＝2，
故{bn}的前n项和Tn＝
＝2n－1.
点睛:本题考查等差数列的基本量运算求通项公式以及等比数列的前n项和,属于基础题. 在数列求和中，最常见最基本的求和就是等差数列、等比数列中的求和，这时除了熟练掌握求和公式外还要熟记一些常见的求和结论，再就是分清数列的项数，比如题中给出的
,以免在套用公式时出错．
练习册系列答案
阅读快车系列答案
相关题目
