题目内容
已知x,y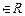 ,且x+2y≥1,则二次函数式u=x2+y2+4x-2y的最小值______.
,且x+2y≥1,则二次函数式u=x2+y2+4x-2y的最小值______.
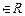 ,且x+2y≥1,则二次函数式u=x2+y2+4x-2y的最小值______.
,且x+2y≥1,则二次函数式u=x2+y2+4x-2y的最小值______. 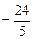
因为x,y 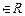 ,且x+2y≥1,所以表示的平面区域如下图所示:
,且x+2y≥1,所以表示的平面区域如下图所示:
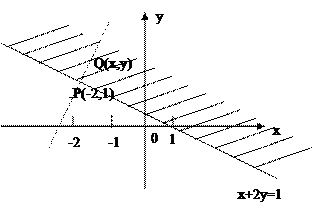
函数式u=x2+y2+4x-2y=(x+2)2+(y-1)2-5,当x=-2,y=1时,即取P(-2,1)时,u的值为最小,
但是点P(-2,1)不在区域x+2y≥1内,所以函数u=x2+y2+4x-2y不在点P处取得最小值。但是,当整体V=(x+2)2+(y-1)2取得最小值时,u就取得最小值,即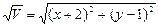 取最小值。可以理解为在区域x+2y≥1上任取一点Q(x,y)到点P(-2,1)的距离的最小值,故作直线PQ垂直于直线:x+2y=1,垂足为Q就是要求的符合条件的点。
取最小值。可以理解为在区域x+2y≥1上任取一点Q(x,y)到点P(-2,1)的距离的最小值,故作直线PQ垂直于直线:x+2y=1,垂足为Q就是要求的符合条件的点。
又LPQ:2X-Y+5="0," 由 得点Q的坐标为Q(
得点Q的坐标为Q(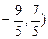
把Q(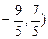 代入u=x2+y2+4x-2y=(x+2)2+(y-1)2-5=(
代入u=x2+y2+4x-2y=(x+2)2+(y-1)2-5=(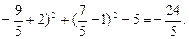
即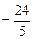 为所求的最小值
为所求的最小值
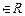 ,且x+2y≥1,所以表示的平面区域如下图所示:
,且x+2y≥1,所以表示的平面区域如下图所示: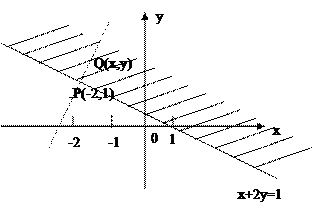
函数式u=x2+y2+4x-2y=(x+2)2+(y-1)2-5,当x=-2,y=1时,即取P(-2,1)时,u的值为最小,
但是点P(-2,1)不在区域x+2y≥1内,所以函数u=x2+y2+4x-2y不在点P处取得最小值。但是,当整体V=(x+2)2+(y-1)2取得最小值时,u就取得最小值,即
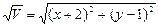 取最小值。可以理解为在区域x+2y≥1上任取一点Q(x,y)到点P(-2,1)的距离的最小值,故作直线PQ垂直于直线:x+2y=1,垂足为Q就是要求的符合条件的点。
取最小值。可以理解为在区域x+2y≥1上任取一点Q(x,y)到点P(-2,1)的距离的最小值,故作直线PQ垂直于直线:x+2y=1,垂足为Q就是要求的符合条件的点。又LPQ:2X-Y+5="0," 由
 得点Q的坐标为Q(
得点Q的坐标为Q(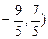
把Q(
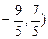 代入u=x2+y2+4x-2y=(x+2)2+(y-1)2-5=(
代入u=x2+y2+4x-2y=(x+2)2+(y-1)2-5=(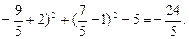
即
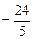 为所求的最小值
为所求的最小值
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -
-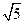 >
>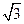
 +
+
 >3+
>3+
 >8
>8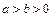 ,则下列不等式中总成立的是
,则下列不等式中总成立的是


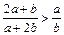
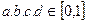
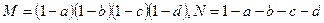 ,
, 的图象经过点
的图象经过点 和
和 两点,
两点, ,则
,则 的取值范围是 ( )
的取值范围是 ( )


