Question

【题目】选修4－4：坐标系与参数方程

已知曲线C的极坐标方程是，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．

（1）求曲线C的直角坐标方程和直线L的普通方程；

（2）设点P（m，0），若直线L与曲线C交于两点A，B，且，求实数m的值．

Answer 1

【答案】（1），；（2）．

【解析】

试题分析：第一问利用极坐标与平面直角坐标之间的转换关系，将曲线的极坐标方程转化为平面直角坐标方程，消参将直线的参数方程转化为普通方程，第二问根据直线的参数方程当中参数的几何意义，将直线的参数方程与曲线的平面直角坐标方程联立，消元化为关于的一元二次方程，结合根与系数之间的关系，得到关于的等量关系式，求得结果，一定要验证两个交点的存在性．

试题解析：（1）曲线C的极坐标方程是，化为，

可得直角坐标方程：．

直线L的参数方程是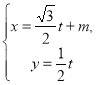（t为参数），

消去参数t可得．

把（t为参数），代入方程：，

化为，

由，解得-1<m<3．．

，，

解得．又满足．∴实数．