Question

设函数f（x）=

1

4

x⁴+bx²+cx+d，当x=t₁时，f（x）有极小值．
（1）若b=-6时，函数f（x）有极大值，求实数c的取值范围；
（2）在（1）的条件下，若存在实数c，使函数f（x）在闭区间[m-2，m+2]上单调递增，求m的取值范围；
（3）若函数f（x）只有一个极值点，且存在t₂∈（t₁，t₁+1），使f′（t₂）=0，证明：函数g（x）=f（x）-

1

2

x²+t₁x在区间（t₁，t₂）内最多有一个零点．

Answer 1

分析：（1）利用条件得f′（x）=0有三个互异的实根，在对导函数求导，根据极值来下结论．
（2）先利用导函数求出函数f（x）的单调递增区间，再让闭区间[m-2，m+2]是所求区间的子集即可求m的取值范围．
（3）函数f（x）只有一个极值点，就是在导函数为0的根左右两侧的函数值异号的根只有一个x=t₁．所以在x=t₂两侧同号，t₁＜x＜t₂，求得（x-t₂）²-1＜0推出函数g（x）在（t₁，t₂）内单调减即可得结论．

解答：解：（1）因为f（x）=

1

4

x⁴+bx²+cx+d，所以h（x）=f′（x）=x³-12x+c．（2分）
由题设，方程h（x）=0有三个互异的实根．
考察函数h（x）=x³-12x+c，则h′（x）=0，得x=±2．

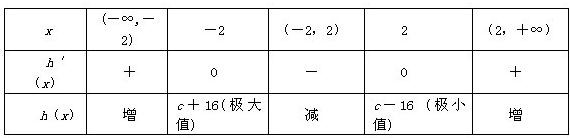
所以

c+16＞0 c-16＜0.

故-16＜c＜16．（5分）
（2）存在c∈（-16，16），使f′（x）≥0，即x³-12x≥-c，（*）
所以x³-12x＞-16，即（x-2）²（x+4）＞0（*）在区间[m-2，m+2]上恒成立．（7分）
所以[m-2，m+2]是不等式（*）解集的子集．
所以

m-2＞-4 m+2＜2

或m-2＞2，即-2＜m＜0，或m＞4．（9分）
（3）由题设，可得存在α，β∈R，使f′（x）=x³+2bx+c=（x-t₁）（x²+αx+β），
且x²+αx+β≥0恒成立．（11分）
又f?（t₂）=0，且在x=t₂两侧同号，
所以f?（x）=（x-t₁）（x-t₂）²．（13分）
另一方面，g′（x）=x³+（2b-1）x+t₁+c
=x³+2bx+c-（x-t₁）=（x-t₁）[（x-t₂）²-1]．
因为t₁＜x＜t₂，且t₂-t₁＜1，所以-1＜t₁-t₂＜x-t₂＜0．
所以0＜（x-t₂）²＜1，所以（x-t₂）²-1＜0．
而x-t₁＞0，所以g′（x）＜0，所以g（x）在（t₁，t₂）内单调减．
从而g（x）在（t₁，t₂）内最多有一个零点．（16分）

点评：本题考查利用极值求对应变量的值．可导函数的极值点一定是导数为0的点，但导数为0的点不一定是极值点