Question

（本小题满分14分）

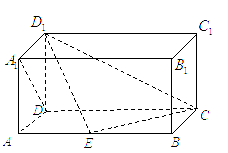如图，在长方体中，，．

   （1）证明：当点在棱上移动时，；

   （2）在棱上是否存在点，使二面角的平面角

为？若存在，求出的长；若不存在，请说明理由．

Answer 1

(Ⅰ)  见解析  (Ⅱ)  

解析:

方法1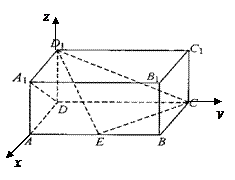：以为原点，、、所在直线分别为轴、轴、轴建立如图所示的空间直角坐标系，则，，，．………1分

设．……………2分

（1）证明： ∵，．

则，∴，即…4分

（2）解：当时，二面角的平面角为．…5分

∵，，……6分

设平面的法向量为，

则，……8分

取，则是平面的一个法向量．…9分

而平面的一个法向量为，   ……10分

要使二面角的平面角为，

则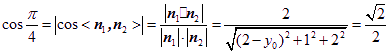，……12分

解得．

∴当时，二面角的平面角为．………14分

方法2：

（1）证明：连结，在长方体中，

∵平面，平面，∴．……1分

∵，则四边形是正方形，∴．……2分

∵，∴平面．………3分

∵平面，∴．……4分

（2）解：当时，二面角的平面角为．  ……5分

连结，过作交于点，连结．…………6分

在长方体中，平面，平面，

∴．……7分∵，∴平面．……8分

∵平面，∴．……………9分

∴为二面角的平面角，即．…………10分

设，则，进而．……11分

在△中，利用面积相等的关系有，，

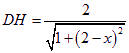∴．   ……12分

在△中，∵，∴．  ………13分

∴，解得．

故当时，二面角的平面角为．……14分