题目内容
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为
为![]() 椭圆上一点,且
椭圆上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.
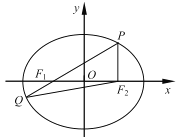
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程及
的方程及![]() 的值;
的值;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围.
的离心率的取值范围.
【答案】(1)![]() ;
;![]() (2)
(2)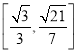
【解析】
(1)把![]() 的坐标代入方程得到
的坐标代入方程得到![]() ,结合
,结合![]() 解出
解出![]() 后可得标准方程.求出直线
后可得标准方程.求出直线![]() 的方程,联立椭圆方程和直线方程后可求
的方程,联立椭圆方程和直线方程后可求![]() 的坐标,故可得
的坐标,故可得![]() 的值.
的值.
(2)因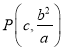 ,故可用
,故可用![]() 表示
表示![]() 的坐标,利用它在椭圆上可得
的坐标,利用它在椭圆上可得![]() 与
与![]() 的关系,化简后可得
的关系,化简后可得![]() 与离心率
与离心率![]() 的关系,由
的关系,由![]() 的范围可得
的范围可得![]() 的范围.
的范围.
(1)因为![]() 垂直于
垂直于![]() 轴,且点
轴,且点![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,![]() ,
,
解得![]() ,
,![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() .
.
所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
将![]() 代入椭圆
代入椭圆![]() 的方程,解得
的方程,解得![]() ,
,
所以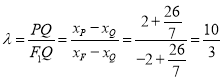 .
.
(2)因为![]() 轴,不妨设
轴,不妨设![]() 在
在![]() 轴上方,
轴上方,![]() ,
,![]() .设
.设![]() ,因为
,因为![]() 在椭圆上,所以
在椭圆上,所以![]() ,解得
,解得![]() ,即
,即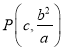 .
.
(方法一)因为![]() ,由
,由![]() 得,
得,![]() ,
,![]() ,解得
,解得![]() ,
,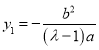 ,所以
,所以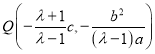 .
.
因为点![]() 在椭圆上,所以
在椭圆上,所以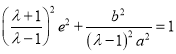 ,即
,即![]() ,所以
,所以![]() ,从而
,从而![]() .
.
因为![]() ,所以
,所以![]() .
.
解得![]() ,
,
所以椭圆![]() 的离心率的取值范围
的离心率的取值范围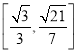 .
.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况.在30名男性驾驶员中,平均车速超过100![]() 额有20人,不超过100
额有20人,不超过100 ![]() 的有10人;在20名女性驾驶员中,平均车速超过100
的有10人;在20名女性驾驶员中,平均车速超过100![]() 的有5人,不超过100
的有5人,不超过100![]() 的有15人.
的有15人.
(1)完成下面的列联表:
平均车速超过100 | 平均车速不超过100 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(2)判断是否有99.5%的把握认为,平均车速超过100![]() 与性别有关.
与性别有关.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()