题目内容
(2013•湖北)设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(2)证明: ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如 .令
.令 的值.
的值.
(参考数据: .
.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(2)证明:
 ;
;(3)设x∈R,记[x]为不小于x的最小整数,例如
 .令
.令 的值.
的值.(参考数据:
 .
.(1)0 (2)见解析 (3)211
(1)由题意得f'(x)=(r+1)(1+x)r﹣(r+1)=(r+1)[(1+x)r﹣1],
令f'(x)=0,解得x=0.
当﹣1<x<0时,f'(x)<0,∴f(x)在(﹣1,0)内是减函数;
当x>0时,f'(x)>0,∴f(x)在(0,+∞)内是增函数.
故函数f(x)在x=0处,取得最小值为f(0)=0.
(2)由(1),当x∈(﹣1,+∞)时,有f(x)≥f(0)=0,
即(1+x)r+1≥1+(r+1)x,且等号当且仅当x=0时成立,
故当x>﹣1且x≠0,有(1+x)r+1>1+(r+1)x,①
在①中,令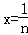 (这时x>﹣1且x≠0),得
(这时x>﹣1且x≠0),得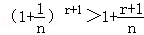 .
.
上式两边同乘nr+1,得(n+1)r+1>nr+1+nr(r+1),
即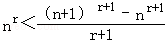 ,②
,②
当n>1时,在①中令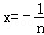 (这时x>﹣1且x≠0),
(这时x>﹣1且x≠0),
类似可得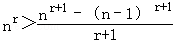 ,③
,③
且当n=1时,③也成立.
综合②,③得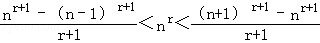 ,④
,④
(3)在④中,令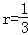 ,n分别取值81,82,83,…,125,
,n分别取值81,82,83,…,125,
得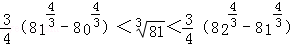 ,
, ,
,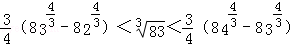 ,…
,…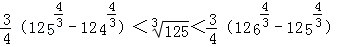 ,
,
将以上各式相加,并整理得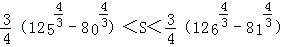 .
.
代入数据计算,可得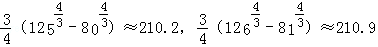
由[S]的定义,得[S]=211.
令f'(x)=0,解得x=0.
当﹣1<x<0时,f'(x)<0,∴f(x)在(﹣1,0)内是减函数;
当x>0时,f'(x)>0,∴f(x)在(0,+∞)内是增函数.
故函数f(x)在x=0处,取得最小值为f(0)=0.
(2)由(1),当x∈(﹣1,+∞)时,有f(x)≥f(0)=0,
即(1+x)r+1≥1+(r+1)x,且等号当且仅当x=0时成立,
故当x>﹣1且x≠0,有(1+x)r+1>1+(r+1)x,①
在①中,令
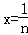 (这时x>﹣1且x≠0),得
(这时x>﹣1且x≠0),得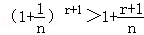 .
.上式两边同乘nr+1,得(n+1)r+1>nr+1+nr(r+1),
即
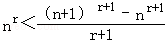 ,②
,②当n>1时,在①中令
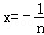 (这时x>﹣1且x≠0),
(这时x>﹣1且x≠0),类似可得
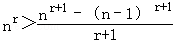 ,③
,③且当n=1时,③也成立.
综合②,③得
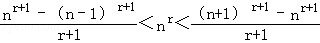 ,④
,④(3)在④中,令
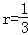 ,n分别取值81,82,83,…,125,
,n分别取值81,82,83,…,125,得
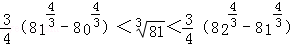 ,
, ,
,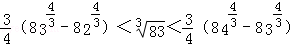 ,…
,…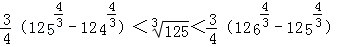 ,
,将以上各式相加,并整理得
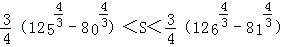 .
.代入数据计算,可得
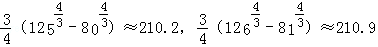
由[S]的定义,得[S]=211.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 为常数且
为常数且
 时,求
时,求 ;
; 满足
满足 ,但
,但 ,则称
,则称 的二阶周期点.证明函数
的二阶周期点.证明函数 ;
;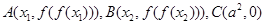 ,记
,记 的面积为
的面积为 ,求
,求 上的最大值和最小值。
上的最大值和最小值。 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 ,都有
,都有 ,则称函数
,则称函数 为函数
为函数 称为周距.
称为周距. 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 上的最大值和最小值.
上的最大值和最小值. (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是________.
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是________. 内有零点,
内有零点, 内有零点,若m为整数,则m的值为 .
内有零点,若m为整数,则m的值为 . ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与 ×S成正比,比例系数为
×S成正比,比例系数为 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S= 时。
时。
 ,使总淋雨量
,使总淋雨量 的两个极值点,且
的两个极值点,且 则b的最大值为_________.
则b的最大值为_________. 在
在 上的最大值为
上的最大值为 ,则函数
,则函数
 个
个 个
个 个
个 个
个