题目内容
用描述法表示所有能被4整除的数的集合 ．
考点：集合的表示法
专题：集合
分析：根据能被4整除的数都可写成4的整数倍，即可得到所求集合．
解答：解：∵能被4整除的数都可写成4的整数倍，
∴所有能被4整除的数的集合可表示为：{x|x=4n，n∈Z}，
故答案为：{x|x=4n，n∈Z}
∴所有能被4整除的数的集合可表示为：{x|x=4n，n∈Z}，
故答案为：{x|x=4n，n∈Z}
点评：本题主要考查了集合表示方法中的描述法，注意表示形式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
由元素1，2，3组成的集合可记为（ ）
| A、{x=1，2，3} | B、{x=1，x=2，x=3} | C、{x|x∈N+，x＜4} | D、{6的质因数} |
| 256 |
| A、{16} |
| B、{-16，16} |
| C、{4} |
| D、{-4，4} |
已知集合 A={x|x2-2x＜0}，B={1，a}，且A∩B有4个子集，则a的取值范围是（ ）
| A、（0，1） | B、（0，2） | C、（0，1）∪（1，2） | D、（-∞，1）（2，+∞） |
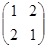的特征值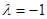
所对应的一个特征向量。