题目内容
已知函数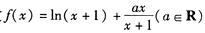
(1)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(2)判断函数f(x)的单调性;
(3)求证: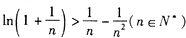
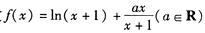
(1)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(2)判断函数f(x)的单调性;
(3)求证:
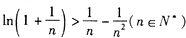
(1) 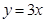 ;(2) 参考解析;(3)参考解析
;(2) 参考解析;(3)参考解析
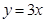 ;(2) 参考解析;(3)参考解析
;(2) 参考解析;(3)参考解析试题分析:(1)已知函数
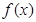 是一个 含对数与分式,以及复合函数,需要正确地对函数
是一个 含对数与分式,以及复合函数,需要正确地对函数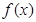 求导,因为函数在x=0处的切线方程,所以将x=0代入导函数,即可求出切线的斜率.再根据横坐标为0,计算出纵坐标,根据点斜式即可写出切线方程.
求导,因为函数在x=0处的切线方程,所以将x=0代入导函数,即可求出切线的斜率.再根据横坐标为0,计算出纵坐标,根据点斜式即可写出切线方程.(2)需要判断函数的单调性,要对函数
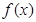 求导,判断导函数的值的正负,所以要根据参数
求导,判断导函数的值的正负,所以要根据参数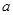 的情况分类讨论后作出判定.
的情况分类讨论后作出判定.(3)解法(一)令
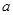 为特殊值,通过函数的单调性得到一个不等式成立,再将x转化为数列中的n的相关的值,再利用一个不等式,从而得到结论.解法(二)根据结论构造函数,通过函数的最值证明恒成立,再将x转化为n的表达式即可.
为特殊值,通过函数的单调性得到一个不等式成立,再将x转化为数列中的n的相关的值,再利用一个不等式,从而得到结论.解法(二)根据结论构造函数,通过函数的最值证明恒成立,再将x转化为n的表达式即可.试题解析:(1)当
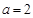 时,
时,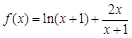 ,
,∴
 ,
,∴
 ,所以所求的切线的斜率为3.又∵
,所以所求的切线的斜率为3.又∵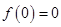 ,所以切点为
,所以切点为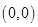 . 故所求的切线方程为:
. 故所求的切线方程为: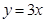 .
.(2)∵
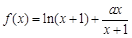
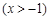 ,
,∴
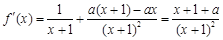 . ①当
. ①当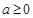 时,∵
时,∵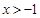 ,∴
,∴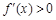 ; 7分
; 7分②当
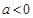 时,
时,由
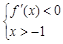 ,得
,得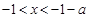 ;由
;由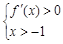 ,得
,得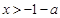 ; 综上,当
; 综上,当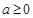 时,函数
时,函数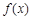 在
在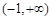 单调递增;
单调递增;当
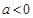 时,函数
时,函数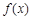 在
在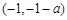 单调递减,在
单调递减,在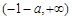 上单调递增.
上单调递增.(3)方法一:由(2)可知,当
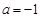 时,
时,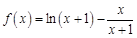 在
在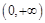 上单调递增. ∴ 当
上单调递增. ∴ 当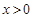 时,
时, ,即
,即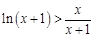 . 令
. 令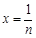 (
(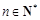 ),则
),则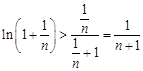 . 另一方面,∵
. 另一方面,∵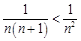 ,即
,即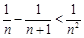 ,
,∴
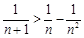 . ∴
. ∴ 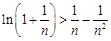 (
(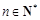 ). 方法二:构造函数
). 方法二:构造函数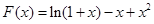 ,
,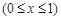 ∴
∴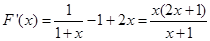 , ∴当
, ∴当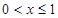 时,
时,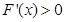 ;
;∴函数
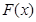 在
在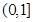 单调递增. ∴函数
单调递增. ∴函数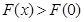 ,即
,即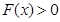
∴
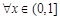 ,
,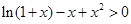 ,即
,即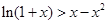
令
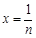 (
(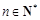 ),则有
),则有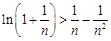 .
.
练习册系列答案
相关题目
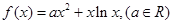
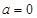 时,求
时,求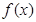 的最小值;
的最小值;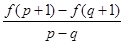 >1恒成立,求实数a的取值范围;
>1恒成立,求实数a的取值范围;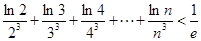 (其中
(其中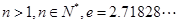 )。
)。 .
.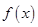 的极值;
的极值;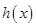 在区间
在区间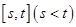 上的取值范围为
上的取值范围为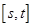 ,则称区间
,则称区间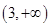 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.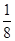 时,证明:方程f(x)=f
时,证明:方程f(x)=f 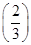 在区间(2,+∞)上有唯一解.
在区间(2,+∞)上有唯一解.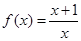 的导函数为
的导函数为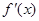 ,则
,则 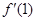 的值为 .
的值为 .
 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.