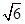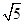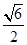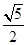题目内容
已知双曲线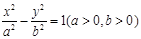 与抛物线
与抛物线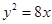 有一个公共的焦点
有一个公共的焦点 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若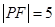 ,则双曲线的渐近线方程为 .
,则双曲线的渐近线方程为 .
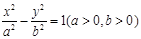 与抛物线
与抛物线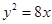 有一个公共的焦点
有一个公共的焦点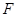 ,且两曲线的一个交点为
,且两曲线的一个交点为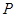 ,若
,若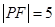 ,则双曲线的渐近线方程为 .
,则双曲线的渐近线方程为 .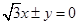
试题分析:由抛物线y2=8x得出其焦点坐标,由|PF|=5结合抛物线的定义得出点P的坐标,从而得到双曲线
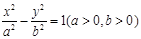 的关于a,b 的方程,求出a,b的值,进而求出双曲线的渐近线方程。解:抛物线y2=8x得出其焦点坐标(2,0)故双曲线的c=2,又|PF|=5,设P(m,n),则|PF|=m+2∴m+2=5,m=3,∴点P的坐标(3,±
的关于a,b 的方程,求出a,b的值,进而求出双曲线的渐近线方程。解:抛物线y2=8x得出其焦点坐标(2,0)故双曲线的c=2,又|PF|=5,设P(m,n),则|PF|=m+2∴m+2=5,m=3,∴点P的坐标(3,±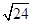 )∴a 2+b 2=4,
)∴a 2+b 2=4,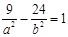 解得:a 2=1,b 2=3则双曲线的渐近线方程为
解得:a 2=1,b 2=3则双曲线的渐近线方程为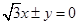 故答案为
故答案为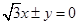 。
。点评:本题主要考查了抛物线的简单性质,双曲线的简单性质,抛物线的定义等.解答的关键是学生对圆锥曲线基础知识掌握的熟练程度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
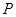 到两点
到两点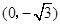 ,
,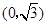 的距离之和等于4,设点
的距离之和等于4,设点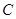 ,直线
,直线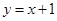 与轨迹
与轨迹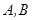 两点.
两点.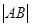 的值.
的值.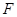 是椭圆
是椭圆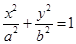 (
(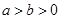 )的左焦点,点
)的左焦点,点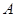 ,
,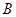 分别是椭圆的左顶点和上顶点,椭圆的离心率为
分别是椭圆的左顶点和上顶点,椭圆的离心率为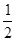 ,点
,点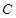 在
在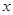 轴上,且
轴上,且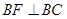 ,过点
,过点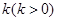 的直线
的直线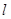 与由三点
与由三点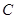 确定的圆
确定的圆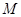 相交于
相交于 ,
, 两点,满足
两点,满足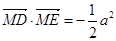 .
.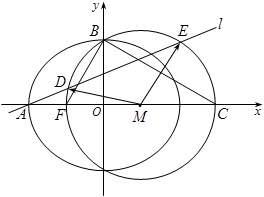
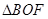 的面积为
的面积为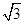 ,求椭圆的方程;
,求椭圆的方程;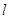 的斜率是否为定值?证明你的结论.
的斜率是否为定值?证明你的结论. 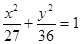 有相同焦点,且经过点
有相同焦点,且经过点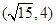 ,求其方程。
,求其方程。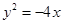 的准线方程是 .
的准线方程是 .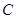 :
: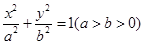 的焦距为
的焦距为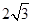 ,离心率为
,离心率为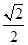 ,其右焦点为
,其右焦点为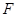 ,过点
,过点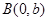 作直线交椭圆于另一点
作直线交椭圆于另一点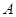 .
.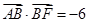 ,求
,求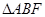 外接圆的方程;
外接圆的方程;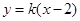 与椭圆
与椭圆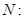
 相交于两点
相交于两点 、
、 ,且
,且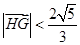 ,求
,求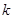 的取值范围.
的取值范围.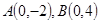 ,动点
,动点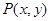 满足
满足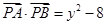 .
.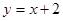 交于点
交于点 、
、 两点 ,求证
两点 ,求证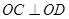 (
(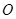 为原点)。
为原点)。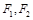 为椭圆
为椭圆 (
(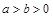 )的两个焦点,过F2作椭圆的弦AB,若
)的两个焦点,过F2作椭圆的弦AB,若 的周长为16,椭圆的离心率
的周长为16,椭圆的离心率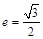 ,则椭圆的方程为( )
,则椭圆的方程为( )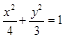


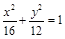
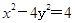 的离心率为
的离心率为