题目内容
11.下列有关命题的说法正确的是( )| A. | 命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0” | |
| B. | “x=3”是“2x2-7x+3=0”成立的充分不必要条件 | |
| C. | 若“p∧(¬q)”为真命题,则“p∧q”也为真命题 | |
| D. | 存在m∈R,使f(x)=(m-1)${x}^{{m}^{2}}$-4m+3是幂函数,且在(0,+∞)上是递增的 |
分析 利用命题的否定判断A的正误;利用充要条件判断B的正误;利用命题的真假判断C的正误;幂函数的定义判断D的正误;
解答 解:对于A,命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0”,不满足特称命题与全称命题的否定关系,所以A不正确;
对于B,“x=3”可以推出“2x2-7x+3=0”成立,但是2x2-7x+3=0,不一定有x=3,所以“x=3”是“2x2-7x+3=0”成立的充分不必要条件,所以B正确.
对于C,若“p∧(¬q)”为真命题,说明P,¬q是真命题,则“p∧q”也为假命题,所以C不正确;
对于D,存在m∈R,使f(x)=(m-1)${x}^{{m}^{2}}$-4m+3是幂函数,可得m=2,函数化为:f(x)=x0=1,所函数在(0,+∞)上是递增的是错误的,所以D不正确;
故选:B.
点评 本题考查命题的真假的判断,命题的否定、充要条件、复合命题的真假以及幂函数的性质的应用,基本知识的考查.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
1.已知函数f(x)=cos(2x-$\frac{π}{3}$),g(x)=sin2x,将函数f(x)的图象经过下列哪种可以与g(x) 的图象重合( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
2.阅读下面程序框图,为使输出的数据为11,则①处应填的数字可以为( )
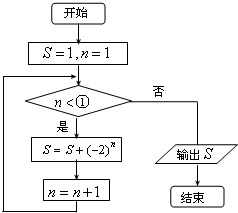

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
6.已知α,β 表示平面,m,n表示直线,给出下列四个命题:
①若α∥β,m?α,n?β,则m∥n; ②若α⊥β,m?α,n?β,则m⊥n;
③若m⊥α,n⊥β,m∥n,则α∥β; ④若m∥α,n∥β,m⊥n,则α⊥β.
其中错误的命题个数为( )
①若α∥β,m?α,n?β,则m∥n; ②若α⊥β,m?α,n?β,则m⊥n;
③若m⊥α,n⊥β,m∥n,则α∥β; ④若m∥α,n∥β,m⊥n,则α⊥β.
其中错误的命题个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.口袋中有20个球,其中白球9个,红球5个,黑球6个,现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是( )
| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
1.已知椭圆M:$\frac{{x}^{2}}{4}$+y2=1的上、下顶点为A,B,过点P(0,2)的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间),则$\overrightarrow{OC}$•$\overrightarrow{OD}$的取值范围( )
| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |
