Question

已知F₁，F₂是椭圆  (a＞b＞0)的左，右焦点，点P是椭圆在y轴右侧上的点，且∠F₁PF₂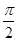＝，记线段PF₁与y轴的交点为Q，O为坐标原点，若△F₁OQ与四边形OF₂PQ的面积之比为1∶2，则该椭圆的离心率等于   

 

Answer 1

【答案】

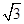－1  

【解析】

试题分析：根据题意，由于F₁，F₂是椭圆 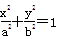 (a＞b＞0)的左，右焦点，点P是椭圆在y轴右侧上的点，且∠F₁PF₂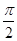＝，且有△F₁OQ与四边形OF₂PQ的面积之比为1∶2，则可知为点P到x轴的距离是Q到x轴距离的3：2倍，那么结合勾股定理可知该椭圆的离心率等于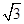－1 ，故答案为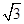－1 。

考点：椭圆的性质

点评：主要是考查了椭圆的方程与性质的运用，属于中档题。