题目内容
(本小题满分14分)如图,已知四面体ABCD的四个面均为锐角三角形,E、F、G、H分别为边AB、BC、CD、DA上的点,BD∥平面EFGH,且EH=FG.
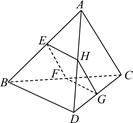
(1) 求证:HG∥平面ABC;
(2) 请在面ABD内过点E作一条线段垂直于AC,并给出证明.

(1) 求证:HG∥平面ABC;
(2) 请在面ABD内过点E作一条线段垂直于AC,并给出证明.
(1) 证明:因为BD∥平面EFGH,平面BDC∩平面EFGH=FG,所以BD∥FG.
同理BD∥EH,又EH=FG, 所以四边形EFGH为平行四边形, 所以HG∥EF.
又HG?平面ABC,EF?平面ABC, 所以HG∥平面ABC. (6分)
(6分)
(2) 解:在平面ABC内过点E作EP⊥AC,且交AC于点P,
在平面ACD内过点P作PQ⊥AC,且交AD于点Q,
连结EQ,则EQ即为所求线段. (10分)
同理BD∥EH,又EH=FG, 所以四边形EFGH为平行四边形, 所以HG∥EF.
又HG?平面ABC,EF?平面ABC, 所以HG∥平面ABC.
 (6分)
(6分)(2) 解:在平面ABC内过点E作EP⊥AC,且交AC于点P,
在平面ACD内过点P作PQ⊥AC,且交AD于点Q,
连结EQ,则EQ即为所求线段. (10分)
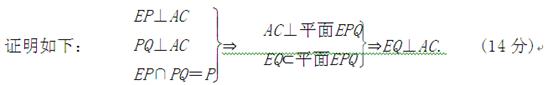 略
略
练习册系列答案
相关题目
 平面EFG
平面EFG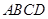 为矩形,且
为矩形,且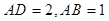 ,
,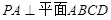 ,
,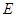 为
为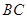 上的动点。
上的动点。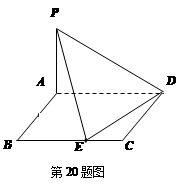
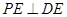 ;
;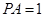 ,在线段
,在线段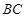 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角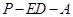 的平面角大小为
的平面角大小为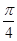 。试确定点E的位置。
。试确定点E的位置。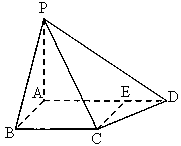
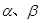 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面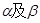 之外的两条不同的直线,给出四个论断: ①m⊥n,②
之外的两条不同的直线,给出四个论断: ①m⊥n,②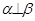 ,③
,③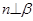 ,④
,④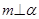 。
。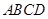 中,
中,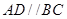 ,
,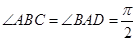 ,
,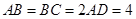 ,
,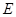 、
、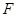 分别是
分别是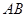 、
、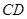 上的动点,且
上的动点,且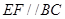 ,设
,设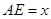 (
(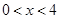 )。沿
)。沿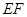 将梯形
将梯形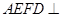 平面
平面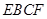 ,如图(2)。
,如图(2)。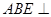 平面
平面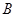 、
、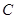 、
、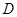 、
、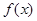 ,求
,求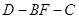 的正弦值.
的正弦值.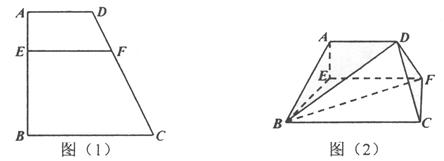
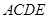 所在的平面垂直于平面
所在的平面垂直于平面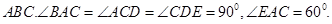
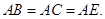
 的中点为
的中点为 ,求证
,求证 ∥面
∥面
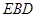 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值
的余弦值
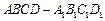 中,设
中,设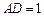 ,
,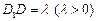 ,
, 上存在点
上存在点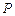 满足
满足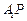
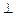 平面
平面 ,求实数
,求实数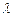 的取值范围
的取值范围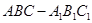 中,底面
中,底面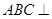 侧面
侧面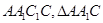 为等边三角形,
为等边三角形,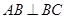 且AB=BC,三棱锥
且AB=BC,三棱锥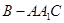 的体积为
的体积为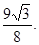

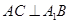 ;
;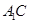 与平面BAA1所成角的正弦值.
与平面BAA1所成角的正弦值.