题目内容
【题目】已知椭圆
的中心在坐标原点，离心率等于
，它的一个长轴端点恰好是抛物线
的焦点.
（1）求椭圆的标准方程；
（2）已知
、
（
）是椭圆上的两点，
是椭圆上位于直线
两侧的动点，且直线
的斜率为.
①求四边形APBQ的面积的最大值；
②求证：
.
【答案】（1）
；（2）①
；②证明见解析.
【解析】
（1）设椭圆C的方程，再根据抛物线
的焦点坐标，和椭圆离心率，则可求出椭圆C的方程的解析式.
（2）①先求出m的值，设
，和直线AB的方程，再联立直线AB的方程和由（1）求得的椭圆方程，得到
，可求出t的范围，再根据韦达定理可得
，则四边形APBQ的面积的最大值可求，②由①得P点坐标，再根据斜率公式写出
,
,再将
化简即可得
则
可证.
（1）由题意设椭圆
的方程为
，
因为抛物线的焦点坐标为
，则
，
由
，
∴椭圆C的方程为.
（2）①当
时，解得
，
，
设，直线AB的方程为
，
，
，
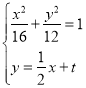由
，解得
，
由韦达定理得
.
，
由此可得：四边形APBQ的面积
，
∴当
时，.
②
，
，
，
即
，
.
考前必练系列答案【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查，张三提供了该县某山羊养殖场年养殖数量
单位：万只
与相应年份
序号的数据表和散点图
如图所示，根据散点图，发现y与x有较强的线性相关关系，李四提供了该县山羊养殖场的个数
单位：个关于x的回归方程
．
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊 |
|
|
|
|
|
|
|
|
|
根据表中的数据和所给统计量，求y关于x的线性回归方程参考统计量：
，
；
试估计：
该县第一年养殖山羊多少万只
到第几年，该县山羊养殖的数量与第一年相比缩小了？
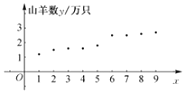
附：对于一组数据
，
，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
．
【题目】为了解某品种一批树苗生长情况，在该批树苗中随机抽取了容量为120的样本，测量树苗高度（单位：cm），经统计，其高度均在区间[19，31]内，将其按[19，21)，[21，23)，[23，25)，[25，27)，[27，29)，[29，31]分成6组，制成如图所示的频率分布直方图．其中高度为27 cm及以上的树苗为优质树苗．
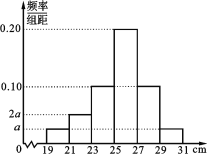
（1）求图中a的值；
（2）已知所抽取的这120棵树苗来自于A，B两个试验区，部分数据如下列联表：
A试验区 | B试验区 | 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整，并判断是否有99.9%的把握认为优质树苗与A，B两个试验区有关系，并说明理由；
（3）用样本估计总体，若从这批树苗中随机抽取4棵，其中优质树苗的棵数为X，求X的分布列和数学期望EX．
下面的临界值表仅供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
，其中
．）
【题目】
某位同学进行寒假社会实践活动，为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究，他分别记录了1月11日至1月15日的白天平均气温
（°C）与该奶茶店的这种饮料销量
（杯），得到如下数据：
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
（1）若从这五组数据中随机抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；
（2）请根据所给五组数据，求出y关于x的线性回归方程
．
（参考公式：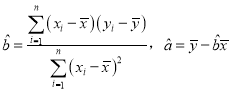
．）
