题目内容
定义在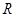 上的函数
上的函数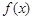 ,对任意
,对任意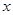 均有
均有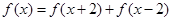 且
且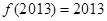 ,则
,则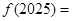 .
.
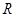 上的函数
上的函数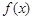 ,对任意
,对任意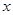 均有
均有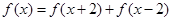 且
且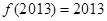 ,则
,则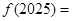 .
.2013
试题分析:∵
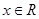 ,
,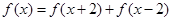 ,∴
,∴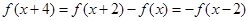 ,
,∴
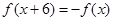 ,∴
,∴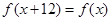 ,则函数
,则函数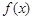 是以12为周期的函数,∵
是以12为周期的函数,∵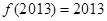 ,
,∴
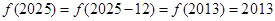 .
.点评:这类问题求解的关键是审题,弄清问题中涉及函数的哪几个性质,有时是函数的几个性质结合运用,本题只用周期函数的性质求解.

练习册系列答案
相关题目
题目内容
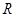 上的函数
上的函数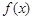 ,对任意
,对任意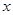 均有
均有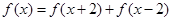 且
且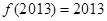 ,则
,则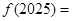 .
.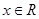 ,
,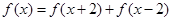 ,∴
,∴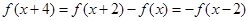 ,
,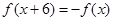 ,∴
,∴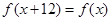 ,则函数
,则函数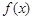 是以12为周期的函数,∵
是以12为周期的函数,∵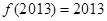 ,
,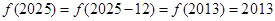 .
.