题目内容
【题目】如图，AB是圆O的直径，C是圆上的点，平面PAC⊥平面ABC，PA⊥AB.
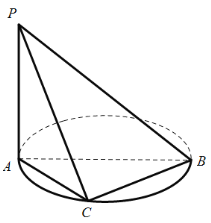
（1）求证：PA⊥平面ABC；
（2）若PA=AC=2，求点A到平面PBC的距离．
【答案】（1）见解析（2）
【解析】
（1）证明BC⊥平面PAC得到BC⊥PA，结合题目条件PA⊥AB得到证明.
（2）令BC＝a，利用等体积法
，解得距离.
（1）∵AB是圆O的直径，∴ AC⊥BC ，
又平面PAC⊥平面ABC且平面PAC
平面ABC＝AC，
∴ BC⊥平面PAC，
平面
，∴ BC⊥PA，
又PA⊥AB，
，∴ PA⊥平面ABC.
（2）由（1）知PA⊥AC，BC⊥PC，令BC＝a，∵PA=AC=2，∴PC＝2，
∴ 
，
，
设点A到平面PBC的距离为d，
则由得：
，∴ 
.
即A到平面PBC的距离为.
练习册系列答案
相关题目
