题目内容
 已知全集U=R,集合A={x|1≤(
已知全集U=R,集合A={x|1≤(| 1 |
| 2 |
| ln(4-x) | ||
|
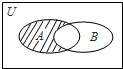
(1)求阴影部分表示的集合D;
(2)若集合C={x|4-a<x<a},且C⊆(A∪B),求实数a的取值范围.
分析:(1)将阴影部分表示的集合,利用集合的基本计算求D;
(2)利用条件C⊆(A∪B),即可求实数a的取值范围.
(2)利用条件C⊆(A∪B),即可求实数a的取值范围.
解答:解:(1)集合A={x|1≤(
)1-x≤4}={x|1≤x≤3},B={x|y=
}={x|
}={x|2<x<4},
则阴影部分的 集合D=A∩CUB={x|1≤x≤2}.
(2)∵A={x|1≤x≤3},B={x|2<x<4},
∴A∪B={x|1≤x<4},
∵C={x|4-a<x<a},且C⊆(A∪B),
∴当4-a≥a,即a≤2时,C=∅,满足题意,
当4-a<a,即a>2时,则满足
,
解得:2<a≤3.
∴实数a的取值范围是a≤3.
| 1 |
| 2 |
| ln(4-x) | ||
|
|
则阴影部分的 集合D=A∩CUB={x|1≤x≤2}.
(2)∵A={x|1≤x≤3},B={x|2<x<4},
∴A∪B={x|1≤x<4},
∵C={x|4-a<x<a},且C⊆(A∪B),
∴当4-a≥a,即a≤2时,C=∅,满足题意,
当4-a<a,即a>2时,则满足
|
解得:2<a≤3.
∴实数a的取值范围是a≤3.
点评:本题主要考查集合的基本运算以及集合关系的应用,比较基础.

练习册系列答案
相关题目