题目内容
8.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)+cos(ωx-$\frac{π}{6}$)(ω>0)的最小正周期为π.(1)求函数f(x)的单调递减区间,其图象对称轴的方程和对称中心的坐标;
(2)作出该函数在一个周期内的简图;
(3)求函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上的最大值和最小值.
分析 (1)由已知条件得到f(x)=3sin(ωx+$\frac{π}{3}$),由此能求出函数f(x)的单调递减区间,其图象对称轴的方程和对称中心的坐标.
(2)由f(x)=3sin(ωx+$\frac{π}{3}$),利用“五点法“能作出该函数在一个周期内的简图.
(3)由f(x)=3sin(2x+$\frac{π}{3}$),x∈[-$\frac{π}{4}$,$\frac{π}{4}$],得$2x+\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],由此能求出函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上的最大值和最小值.
解答 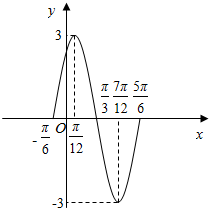 解:(1)f(x)=2sin(ωx+$\frac{π}{3}$)+cos(ωx-$\frac{π}{6}$)(ω>0)
解:(1)f(x)=2sin(ωx+$\frac{π}{3}$)+cos(ωx-$\frac{π}{6}$)(ω>0)
=2sin(ωx+$\frac{π}{3}$)+sin(ωx+$\frac{π}{3}$)
=3sin(ωx+$\frac{π}{3}$),
∵函数f(x)=2sin(ωx+$\frac{π}{3}$)+cos(ωx-$\frac{π}{6}$)(ω>0)的最小正周期为π,
∴$\frac{2π}{ω}$=π,解得ω=2,
∴f(x)=sin(2x+$\frac{π}{3}$),
∴由$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,k∈Z,得到$\frac{π}{12}+kπ≤x≤\frac{7π}{12}+kπ$,k∈Z,
∴函数f(x)的单调递减区间为[$\frac{π}{12}+kπ,\frac{7π}{12}+kπ$],k∈Z.
由$2x+\frac{π}{3}=\frac{π}{2}+kπ$,k∈Z,得到f(x)图象对称轴的方程为:x=$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
由2x+$\frac{π}{3}$=kπ,k∈Z,得x=$\frac{kπ}{2}-\frac{π}{6}$,k∈Z,∴对称中心($\frac{kπ}{2}-\frac{π}{6}$,0),k∈Z.
(2)列表:
| x | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| 2x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 0 | 3 | 0 | -3 | 0 |
(3)∵f(x)=3sin(2x+$\frac{π}{3}$),x∈[-$\frac{π}{4}$,$\frac{π}{4}$],∴$2x+\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴f(x)min=3sin(-$\frac{π}{6}$)=-$\frac{3}{2}$,
f(x)max=3sin($\frac{π}{2}$)=3.
∴函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上的最大值为3,最小值为-$\frac{3}{2}$.
点评 本题考查三角函数的单调递减区间,其图象对称轴的方程、对称中心的坐标、函数在一个周期内的简图、函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上的最大值和最小值的求法,是中档题,解题时要注意三角函数的性质和五点法作图的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 10π | B. | 12π | C. | 22π | D. | 25π |
(1)定义域为R,值域为[1,+∞);
(2)图象关于x=2对称
(3)函数在(-∞,0)上是减函数
请写出函数f(x)的一个解析式(x-2)2+1(只要写出一个即可)
| A. | 在$[\frac{π}{6},\frac{2π}{3}]$上是增函数 | |
| B. | 图象关于直线$x=\frac{5π}{12}$对称 | |
| C. | 图象关于点$(-\frac{π}{3},0)$对称 | |
| D. | 把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个单位,所得函数图象关于y轴对称 |