题目内容
据民生所望,相关部门对所属单位进行整治性核查,标准如下表:
规定初查累计权重分数为10分或9分的不需要复查并给予奖励,10分的奖励18万元;9分的奖励8万元;初查累计权重分数为7分及其以下的停下运营并罚款1万元;初查累计权重分数为8分的要对不合格指标进行复查,最终累计权重得分等于初查合格部分与复查部分得分的和,最终累计权重分数为10分方可继续运营,否则停业运营并罚款1万元.
(1)求一家单位既没获奖励又没被罚款的概率;
(2)求一家单位在这次整治性核查中所获金额X(万元)的分布列和数学期望(奖励为正数,罚款为负数).
(1)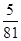 ;(2)分布列详见解析,
;(2)分布列详见解析,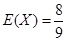 .
.
解析试题分析:本题主要考查离散型随机变量的分布列与数学期望等基础知识,考查综合分析问题解决问题的能力,考查运用概率知识解决简单实际问题的能力,考查计算能力.第一问,分析题意:只有得8分的情况既没有奖励又没有罚款,但是得8分时需要复查不合格指标项,所以符合题意的情况有:①甲的4个指标项合格,乙的2个指标项不合格,并对乙的2个指标项进行复查,②甲的4个指标项有3个合格,1个不合格,乙的2个指标项合格并对甲中不合格的1个指标项进行复查;第二问,通过已知条件得出,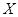 有4种情况:当
有4种情况:当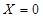 时,表示既没有奖励又没有罚款的情况,也就是第一问的情况;当
时,表示既没有奖励又没有罚款的情况,也就是第一问的情况;当 时,表示累计权重分数为9分,也就是甲的4个指标项都合格,而乙中的2个指标项只有1个合格;当
时,表示累计权重分数为9分,也就是甲的4个指标项都合格,而乙中的2个指标项只有1个合格;当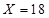 时,表示累计权重分数为10分,也就是说甲乙中的所以指标项都合格的情况;当
时,表示累计权重分数为10分,也就是说甲乙中的所以指标项都合格的情况;当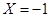 时,表示累计权重分数为7分,也就是甲中的4个指标项有3个合格1个不合格,乙中的2个指标项1个合格1个不合格,利用分析的情况列出概率表达式,列出分布列,利用期望的计算公式求数学期望.
时,表示累计权重分数为7分,也就是甲中的4个指标项有3个合格1个不合格,乙中的2个指标项1个合格1个不合格,利用分析的情况列出概率表达式,列出分布列,利用期望的计算公式求数学期望.
试题解析:记“初查阶段甲类的一个指标项合格”为事件 ,“初查阶段乙类的一个指标项合格”为事件
,“初查阶段乙类的一个指标项合格”为事件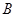 ,“复查阶段一个指标项合格”为事件
,“复查阶段一个指标项合格”为事件 ,则
,则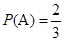 ,
,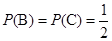 .
.
(Ⅰ)记“一家单位既没获奖励又没被罚款”为事件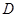 ,则
,则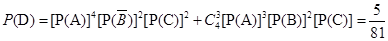 . 4分
. 4分
(Ⅱ)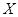 的可能取值为-1,0,8,18.
的可能取值为-1,0,8,18.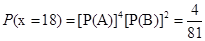 ,
,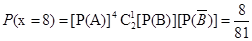 ,
,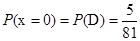 ,
,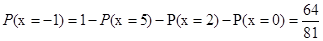 .
.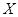 的分布列为
的分布列为X -1 0 8 18 P 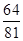
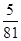
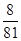
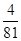
10分 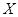 的数学期望
的数学期望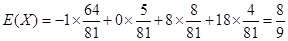 (万元). 12分
(万元). 12分
考点:离散型随机变量的分布列和数学期望.

在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
(2)若这2人来自区域A,D,并记来自区域A队员中的人数为X,求随机变量X的分布列及数学期望.
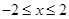 ,
,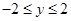 ,点
,点 的坐标为
的坐标为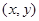 .
.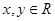 时,点
时,点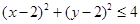 的概率;
的概率;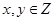 时,点
时,点 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取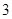 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中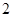 题便通过考查.已知
题便通过考查.已知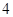 题能正确完成,
题能正确完成,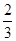 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.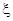 和文科考生乙正确完成题数
和文科考生乙正确完成题数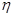 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望;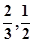 且每棵树是否存活互不影响,求移栽的5棵树中:
且每棵树是否存活互不影响,求移栽的5棵树中: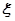 的分布列与期望.
的分布列与期望.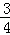 、
、 、
、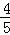 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.