题目内容
某足球俱乐部2013年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。
(Ⅰ)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。
(Ⅰ)小李第一次参加测试就合格的概率为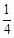 ;(Ⅱ)则x的分布列为
;(Ⅱ)则x的分布列为
小李10月份参加测试的次数x的数学期望为x 1 2 3 4 P 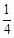

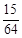
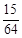
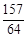 .
.
解析试题分析:(Ⅰ)求小李第一次参加测试就合格的概率,由题意小李4次测试每次合格的概率组成一个公差为 的等差数列,可设第一次参加测试就合格的概率为
的等差数列,可设第一次参加测试就合格的概率为 ,则小李四次测试合格的概率依次为
,则小李四次测试合格的概率依次为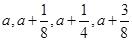 ,而他直到第二次测试才合格的概率为
,而他直到第二次测试才合格的概率为 ,即
,即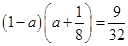 ,解得
,解得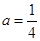 或
或 ,又因为他第一次测试合格的概率不超过
,又因为他第一次测试合格的概率不超过 ,可舍去
,可舍去 ;(Ⅱ)求小李10月份参加测试的次数x的分布列和数学期望,小李10月份参加测试的次数为
;(Ⅱ)求小李10月份参加测试的次数x的分布列和数学期望,小李10月份参加测试的次数为 ,则
,则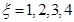 ,小李四次考核每次合格的概率依次为
,小李四次考核每次合格的概率依次为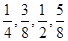 ,根据相互独立事件同时发生的概率,得到分布列和期望.
,根据相互独立事件同时发生的概率,得到分布列和期望.
试题解析:(Ⅰ)设小李四次测试合格的概率依次为:
a, a+ , a+
, a+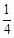 , a+
, a+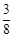 (a≤
(a≤ ), (2分)
), (2分)
则(1-a)(a+ )=
)= ,即
,即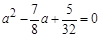 ,
,
解得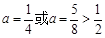 (舍), (5分)
(舍), (5分)
所以小李第一次参加测试就合格的概率为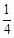 ; (6分)
; (6分)
(Ⅱ)因为P(x=1)=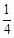 , P(x=2)=
, P(x=2)= ,P(x=3)=
,P(x=3)=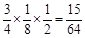 ,
,
P(x=4)=1-P(x=1)-P(x=2)-P(x=3)=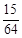 , (8分)
, (8分)
则x的分布列为
(10分)x 1 2 3 4 P 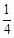

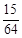
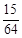
所以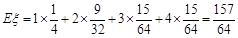 ,
,
即小李10月份参加测试的次数x的数学期望为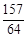 . (12分)
. (12分)
考点:相互独立事件的概率乘法公式.

 应用题作业本系列答案
应用题作业本系列答案为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令的赞成人数如下表:
| 月收入 |  | [25,35) | [35,45) |  |  |  |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 8 | 5 | 2 | 1 |
(Ⅰ)根据已知条件完成下面的2×2列联表,有多大的把握认为赞不赞成楼市限购令与收入高低有关?
已知:
 ,
,当
 <2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
<2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;当
 >2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;
>2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;当
 >3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;
>3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;当
 >6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。
>6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。| | 非高收入族 | 高收入族 | 总计 |
| 赞成 | | | |
| 不赞成 | | | |
| 总计 | | | |
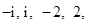 其中
其中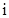 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响). 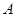 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率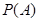 与事件
与事件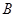 “在四次试验中,
“在四次试验中,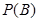 ;
;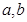 ,求随机变量
,求随机变量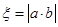 的分布列与数学期望
的分布列与数学期望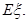


 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求
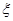 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出