题目内容
已知函数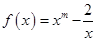 且
且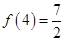 ,
,
(1)求 的值;
的值;
(2)判断 在
在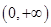 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.
(1)1;(2)单调递增.
解析试题分析:
解题思路:(1)将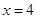 代入
代入 的解析式,求
的解析式,求 值;(2)利用单调性的定义证明即可.
值;(2)利用单调性的定义证明即可.
规律总结:利用单调函数的定义证明函数的单调性的一般步骤:①设值、代值;②作差变形;③判断正负;④下结论.
试题解析:(1)因为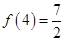 ,所以,所以
,所以,所以 .
.
(2) 在
在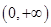 上为单调增函数
上为单调增函数
证明:设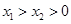 ,则
,则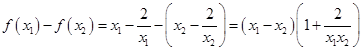 ,
,
因为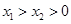 ,所以
,所以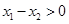 ,
, ,所以
,所以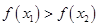 ,
,
所以 在
在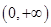 上为单调增函数.
上为单调增函数.
考点:函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
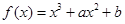 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线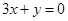 平行.
平行.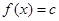 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围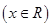 满足
满足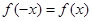 ,
,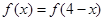 ,且当
,且当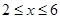 时,
时,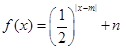 .
.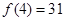 ,求
,求 的值.
的值.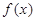 是定义在
是定义在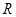 上的奇函数,当
上的奇函数,当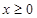 时,
时, .
. ;
;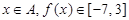 ,求区间
,求区间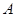 .
.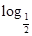 24)的值.
24)的值.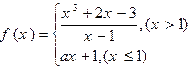 在点
在点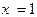 处连续,则
处连续,则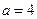 ;
;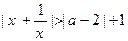 对于一切非零实数
对于一切非零实数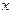 均成立,则实数
均成立,则实数 的取值范围是
的取值范围是 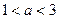
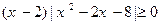 的解集是
的解集是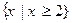
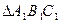 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于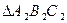 的三个内角的正弦值,则
的三个内角的正弦值,则 是奇函数,则a= .
是奇函数,则a= .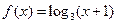 的反函数为
的反函数为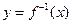 ,则方程
,则方程 的解
的解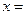 .
.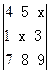 中,元素4的代数余子式大于0,
中,元素4的代数余子式大于0,