题目内容
已知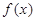 是定义在
是定义在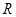 上的奇函数,当
上的奇函数,当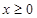 时,
时, .
.
(1)求 ;
;
(2)求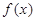 的解析式;
的解析式;
(3)若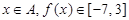 ,求区间
,求区间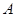 .
.
(1)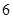 ;(2)
;(2) ;(3)
;(3)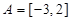 .
.
解析试题分析:(1)根据 是定义在
是定义在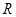 上的奇函数可知:
上的奇函数可知: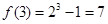 ,
,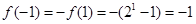 ,从而可得
,从而可得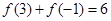 ;(2)根据根据
;(2)根据根据 是定义在
是定义在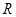 上的奇函数可知:
上的奇函数可知: 再结合
再结合 在
在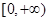 上的解析式,可以得到其在
上的解析式,可以得到其在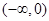 上的解析式:
上的解析式: ,将两者综合,即可得
,将两者综合,即可得 ;(3)由(2)得到的解析式,可知需对
;(3)由(2)得到的解析式,可知需对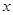 的取值范围分类讨论,从而可以得到关于
的取值范围分类讨论,从而可以得到关于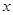 的不等式:当
的不等式:当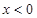 时,
时,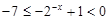 ,解得
,解得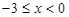 , 当
, 当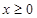 时,
时,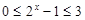 ,解得
,解得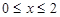 ,因此区间
,因此区间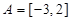 .
.
试题解析:(1)∵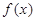 是奇函数,∴
是奇函数,∴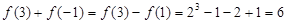 ;
;
(2)∵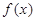 为奇函数,∴当
为奇函数,∴当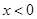 时,
时, ,
,
∴ ;
;
(3)由(2)求得的解析式可知:
当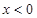 时,
时,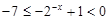 ,解得
,解得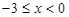 ,
,
当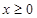 时,
时,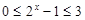 ,解得
,解得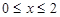 ,∴区间
,∴区间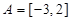 .
.
考点:1.奇函数的性质;2.分类讨论的数学思想.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
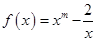 且
且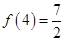 ,
, 的值;
的值; 在
在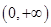 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明. ,当
,当 时,恒有
时,恒有 .
. 为正实数,
为正实数, ,并且
,并且 ,试求
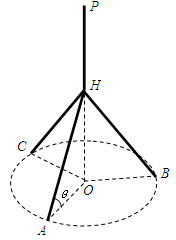
,试求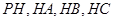 构成,其底端三点
构成,其底端三点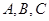 均匀地固定在半径为
均匀地固定在半径为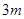 的圆
的圆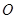 上(圆
上(圆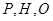 三点相异且共线,
三点相异且共线,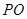 与地面垂直. 现要求点
与地面垂直. 现要求点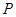 到地面的距离恰为
到地面的距离恰为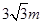 ,记用料总长为
,记用料总长为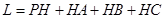 ,设
,设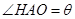 .
.
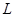 表示为
表示为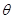 的函数,并注明定义域;
的函数,并注明定义域;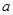 为实数,
为实数,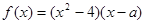 .
.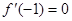 ,求
,求 在
在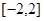 上的最大值和最小值;
上的最大值和最小值;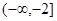 和
和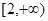 上都是递增的,求
上都是递增的,求 .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围; ,若对任意
,若对任意 恒成立,求
恒成立,求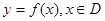 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的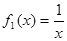 与
与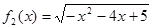 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;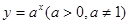 的短距小于1;
的短距小于1;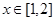 是否存在实数
是否存在实数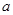 ,使得函数
,使得函数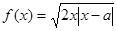 的短距不小于2且长距不大于4.若存在,请求出
的短距不小于2且长距不大于4.若存在,请求出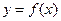
 存在反函数
存在反函数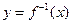
 ,且函数
,且函数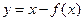 的图像过点
的图像过点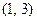 ,则函数
,则函数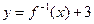 的图像一定过点 .
的图像一定过点 .