题目内容
已知函数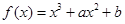 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线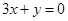 平行.
平行.
(1)求函数 的解析式;
的解析式;
(2)求函数 在区间[0,t](0<t<3)上的最大值和最小值;
在区间[0,t](0<t<3)上的最大值和最小值;
(3)在(1)的结论下,关于x的方程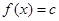 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
(1)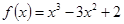 (2)答案见解析 (3)
(2)答案见解析 (3)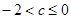
解析试题分析:(1)由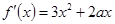 及曲线在
及曲线在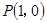 处的切线斜率为
处的切线斜率为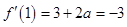 ,即可求得
,即可求得 ,又函数过
,又函数过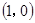 点,即可求的
点,即可求的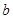 .
.
(2)由(1)易知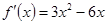 ,令
,令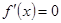 可得
可得 或
或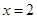 ,然后对
,然后对 进行分类讨论,确定函数
进行分类讨论,确定函数 在
在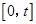 的单调性,即可求出函数
的单调性,即可求出函数 在
在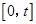
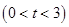 上的最大值和最小值;
上的最大值和最小值;
(3)构造函数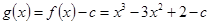 ,研究函数
,研究函数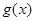 的单调性,列出该方程有两个相异的实根的不等式组,求出实数
的单调性,列出该方程有两个相异的实根的不等式组,求出实数 的取值范围.
的取值范围.
试题解析:(1)因为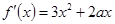 ,曲线在
,曲线在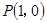 处的切线斜率为
处的切线斜率为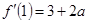 ,即
,即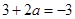 ,所以
,所以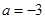 .
.
又函数过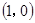 点,即
点,即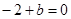 ,所以
,所以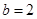 .
.
所以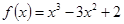 .
.
(2)由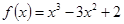 ,
,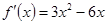 .
.
由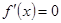 ,得
,得 或
或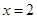 .
.
①当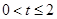 时,在区间
时,在区间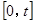 上
上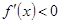 ,
, 在
在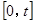 上是减函数,
上是减函数,
所以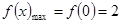 ,
,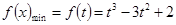 .
.
②当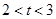 时,当
时,当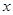 变化时,
变化时, 、
、 的变化情况见下表:
的变化情况见下表: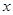
0 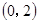
2 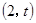
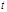
 练习册系列答案
练习册系列答案
寒假作业中国地图出版社系列答案
中考复习攻略南京师范大学出版社系列答案
智多星归类复习测试卷系列答案
智多星模拟加真题测试卷系列答案
毕业升学考卷大集结系列答案
毕业升学冲刺必备方案系列答案
状元坊广东中考备考用书系列答案
百年学典中考风向标系列答案
百校联盟中考冲刺名校模拟卷系列答案
夺A闯关一路领先中考模拟密卷系列答案
相关题目
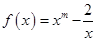 且
且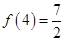 ,
, 的值;
的值; 在
在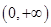 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.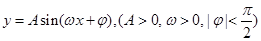 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是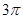 ,又:图象过点
,又:图象过点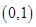 ,
, 的集合;
的集合; ,当
,当 时,恒有
时,恒有 .
. 为正实数,
为正实数, ,并且
,并且 ,试求
,试求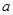 为实数,
为实数,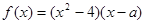 .
.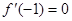 ,求
,求 在
在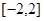 上的最大值和最小值;
上的最大值和最小值;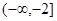 和
和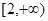 上都是递增的,求
上都是递增的,求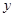 (单位:千克)与销售价格
(单位:千克)与销售价格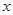 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式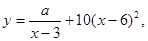 其中
其中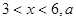 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克. 的值;
的值;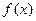 是定义在R上的以3为周期的奇函数,若
是定义在R上的以3为周期的奇函数,若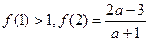 ,则实数
,则实数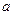 的取值范围是 。
的取值范围是 。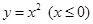 的图象关于直线x-y=0对称,则f(x)=
的图象关于直线x-y=0对称,则f(x)=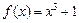 的反函数
的反函数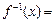 .
.