题目内容
已知椭圆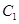 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为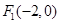 ,
,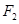
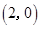 ,点
,点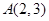 在椭圆
在椭圆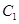 上,过点
上,过点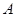 的直线
的直线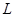 与抛物线
与抛物线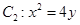 交于
交于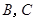 两点,抛物线
两点,抛物线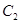 在点
在点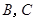 处的切线分别为
处的切线分别为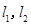 ,且
,且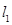 与
与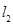 交于点
交于点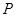 .
.
(1) 求椭圆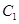 的方程;
的方程;
(2) 是否存在满足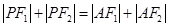 的点
的点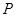 ? 若存在,指出这样的点
? 若存在,指出这样的点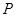 有几个(不必求出点
有几个(不必求出点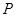 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
(1)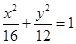 .
(2)满足条件的点
.
(2)满足条件的点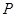 有两个.
有两个.
【解析】
(1)试题分析:解法1:设椭圆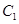 的方程为
的方程为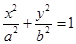
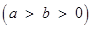 ,依题意:
,依题意: 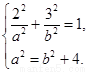
解得: 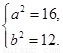 ∴ 椭圆
∴ 椭圆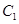 的方程为
的方程为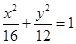 .
.
解法2:设椭圆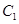 的方程为
的方程为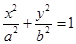
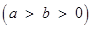 ,根据椭圆的定义得
,根据椭圆的定义得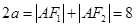 ,即
,即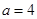 , ∵
, ∵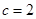 , ∴
, ∴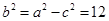 . ∴ 椭圆
. ∴ 椭圆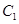 的方程为
的方程为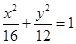 .
.
(2) 解法1:显然直线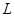 的斜率存在,设直线
的斜率存在,设直线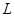 的方程为
的方程为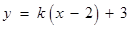 ,
,
由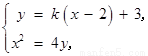 消去
消去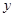 ,得
,得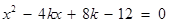 .
.
设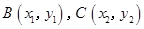 ,则
,则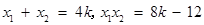 .
.
由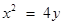 ,即
,即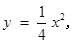 得
得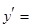
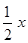 .
.
∴抛物线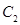 在点
在点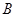 处的切线
处的切线 的方程为
的方程为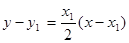 ,即
,即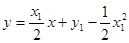 .
.
∵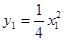 , ∴
, ∴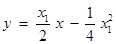 .
.
同理,得抛物线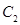 在点
在点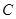 处的切线
处的切线 的方程为
的方程为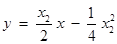 .
.
由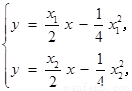 解得
解得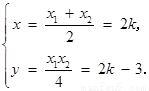
∴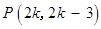 . ∵
. ∵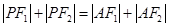 ,
,
∴点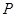 在椭圆
在椭圆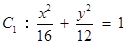 上. ∴
上. ∴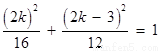 .
.
化简得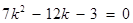 .(*) 由
.(*) 由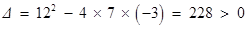 ,
,
可得方程(*)有两个不等的实数根. ∴满足条件的点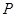 有两个.
有两个.
解法2:设点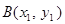 ,
,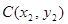 ,
,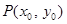 ,由
,由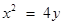 ,即
,即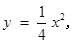 得
得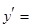
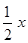 .
.
∴抛物线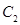 在点
在点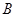 处的切线
处的切线 的方程为
的方程为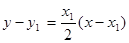 ,
,
即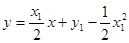 .∵
.∵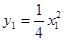 , ∴
, ∴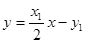 .
.
∵点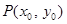 在切线
在切线 上, ∴
上, ∴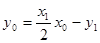 . ①
. ①
同理, 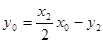 . ② 综合①、②得,点
. ② 综合①、②得,点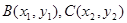 的坐标都满足方程
的坐标都满足方程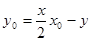 .∵经过
.∵经过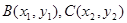 的直线是唯一的,∴直线
的直线是唯一的,∴直线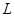 的方程为
的方程为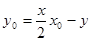 ,
,
∵点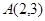 在直线
在直线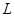 上, ∴
上, ∴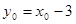 . ∴点
. ∴点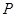 的轨迹方程为
的轨迹方程为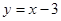 .
.
若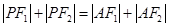 ,则点
,则点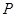 在椭圆
在椭圆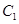 上,又在直线
上,又在直线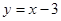 上,∵直线
上,∵直线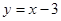 经过椭圆
经过椭圆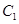 内一点
内一点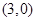 ,∴直线
,∴直线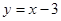 与椭圆
与椭圆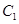 交于两点.
交于两点.
∴满足条件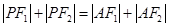 的点
的点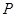 有两个.
有两个.
解法3:设点 ,
,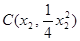 ,则
,则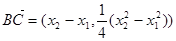 ,
,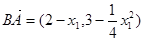 ,
,
∵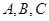 三点共线,
三点共线,  .
. 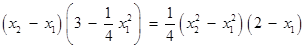
化简得: . ① 由
. ① 由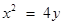 ,即
,即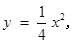 得
得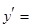
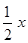 .
.
∴抛物线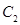 在点
在点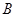 处的切线
处的切线 的方程为
的方程为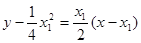 ,即
,即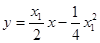 . ②
. ②
同理,抛物线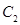 在点
在点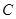 处的切线
处的切线 的方程为
的方程为 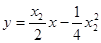 . ③
. ③
设点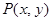 ,由②③得:
,由②③得: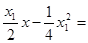
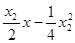 ,而
,而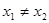 ,则
,则 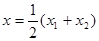 .
.
代入②得
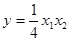 , 则
, 则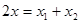 ,
, 代入 ① 得
代入 ① 得
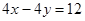 ,
,
即点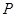 的轨迹方程为
的轨迹方程为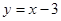 .若
.若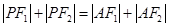 ,则点
,则点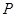 在椭圆
在椭圆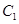 上,而点
上,而点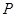 又在直线
又在直线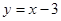 上,∵直线
上,∵直线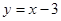 经过椭圆
经过椭圆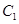 内一点
内一点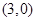 ,
,
∴直线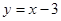 与椭圆
与椭圆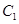 交于两点. ∴满足条件
交于两点. ∴满足条件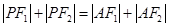 的点
的点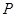 有两个.
有两个.
考点:本题考查了圆锥曲线的方程及直线与圆锥曲线的位置关系
点评:解答此类问题时注意若直线与圆锥曲线有两个交点,对待交点坐标是“设而不求”的原则,要注意应用韦达定理处理这类问题

 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.