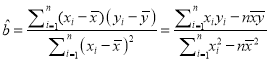题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的标准参数方程;
的标准参数方程;
(2)求![]() 的长;
的长;
(3)以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,设点
轴的正半轴为极轴建立极坐标系,设点![]() 的极坐标为
的极坐标为![]() ;求点
;求点![]() 到线段
到线段![]() 中点
中点![]() 的距离.
的距离.
【答案】(1)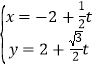 (
(![]() 为参数)(2)
为参数)(2)![]() (3)
(3)![]()
【解析】
(1)求得直线恒过点![]() 且斜率
且斜率![]() 即倾斜角
即倾斜角![]() ,即得直线的参数方程.
,即得直线的参数方程.
(2)将直线的参数方程和曲线方程联立后利用根与系数的关系写出两个交点的横坐标的和与积,利用弦长公式求|AB|的长;
(3)将点P的极坐标化为直角坐标,然后直接利用参数的几何意义求解.
(1)依题,得:直线![]() 过点
过点![]() 且斜率
且斜率![]() 即倾斜角
即倾斜角![]()
![]() 直线
直线![]() 的参数方程化为标准型
的参数方程化为标准型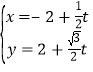 (
(![]() 为参数)
为参数)
(2)将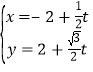 代入曲线
代入曲线![]() 方程得
方程得![]()
设![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
(3)由极坐标与直角坐标互化公式得![]() 直角坐标
直角坐标![]() ,
,
点![]() 在直线上,中点
在直线上,中点![]() 对应参数为
对应参数为![]() ,
,![]()

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 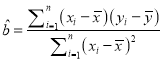
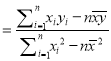 ,
, ![]() )
)